Integrální počet

Kalkul je vedle počtu nejdůležitějšího větve matematické disciplíny analýzy . Vyplynulo to z problému výpočtu plochy a objemu . Integrál je obecný termín pro neurčitý a určitý integrál. Výpočet integrálů se nazývá integrace.

Určitý integrál z funkce přiřadí číslo k němu. Je -li určitý integrál skutečné funkce vytvořen v proměnné , lze výsledek interpretovat v dvojrozměrném souřadném systému jako oblast oblasti, která leží mezi grafem funkce, -osou a omezujícími rovnoběžkami s -osa. Zde se oblasti pod osou počítají jako záporné. Mluví se o orientované povrchové ploše (také povrchové rovnováze ). Tato konvence je zvolena tak, že určitý integrál je lineární mapování${\ displaystyle x}$${\ displaystyle y}$${\ displaystyle x}$je to, co představuje ústřední vlastnost pojmu integrál jak pro teoretické úvahy, tak pro konkrétní výpočty. Tím je také zajištěno, že platí takzvaná hlavní věta diferenciálního a integrálního počtu .

Neurčitý integrál z funkce přiřazuje toto mnoha funkcemi, prvky primitivní funkce se nazývá. Ty se vyznačují tím, že jejich první deriváty odpovídají integrované funkci. Hlavní věta diferenciálního a integrálního počtu poskytuje informace o tom, jak lze určit určité integrály z antiderivativ.

Na rozdíl od diferenciace neexistuje žádný jednoduchý algoritmus, který by pokrýval všechny případy pro integraci i elementárních funkcí . Integrace vyžaduje trénované hádání, použití speciálních transformací ( integrace substitucí , částečná integrace ), vyhledávání v integrální tabulce nebo použití speciálního počítačového softwaru. Integrace často probíhá pouze přibližně pomocí takzvané numerické kvadratury .

V technologii se pro přibližné určení plochy používají takzvané planimetry , ve kterých probíhá souhrn plošných prvků kontinuálně. Takto určenou číselnou hodnotu oblasti lze odečíst na čítači, který je opatřen noniem pro zvýšení přesnosti čtení . Chemici používali k určení integrálu jakékoli oblasti analytické váhy nebo mikrováhy : oblast byla pečlivě vystřižena a zvážena, stejně jako kus stejného papíru o velikosti přesně 10 cm × 10 cm ; trojčlenka vedlo k výsledku.

příběh

Výpočty ploch byly studovány od starověku . V 5. století BC, Eudoxus Knidos vyvinula na metodu vyčerpání založený na nápadu Antiphon , která se skládala z odhadu se podíl ploch pomocí obsažených nebo překrývajících se polygony . Pomocí této metody dokázal určit jak plochu, tak objem některých jednoduchých těles. Archimedes (287–212 př. N. L.) Tento přístup vylepšil, a tak se mu podařilo přesně určit oblast oblasti ohraničené parabolickým obloukem a secantem bez použití konceptu limitu , který v té době ještě nebyl k dispozici; tento výsledek lze snadno převést na integrál dnes známé kvadratické funkce. Odhadl také poměr obvodu k průměru, jako hodnotu mezi a . ${\ displaystyle \ pi}$${\ displaystyle \ textstyle {3 {\ frac {10} {71}}}}$${\ displaystyle \ textstyle {3 {\ frac {10} {70}}}}$

Tato metoda byla také používána ve středověku. V 17. století, Bonaventura Francesco Cavalieri založena na principu Cavalieri , podle kterého obě tělesa mají stejný objem, pokud jsou všechny rovině rovnoběžné úseky mají stejnou plochu. Johannes Kepler ve svém díle Astronomia Nova (1609) použil metody pro výpočet oběžné dráhy Marsu, které by se dnes označovaly jako numerická integrace. Od roku 1612 se pokusil vypočítat objem sudů s vínem. V roce 1615 vydal Stereometria Doliorum Vinariorum ( „ Stereometrie sudů vína“), později také známý jako Keplerova barel pravidlo .

Na konci 17. století se Isaacovi Newtonovi a Gottfriedu Wilhelmu Leibnizovi podařilo nezávisle na sobě vyvinout kameny pro diferenciální počet a objevit tak základní teorii analýzy (historii objevu a spor o prioritu viz článek Nekonečno počet ; pro integrální znak a jeho historii viz integrální znak ). Její práce umožnila abstrakci čistě geometrických myšlenek, a je proto považována za počátek analýzy. Nejznámější jsou díky knize šlechtice Guillauma Françoise Antoina, markýze de L'Hospital , který si vzal soukromé hodiny od Johanna I. Bernoulliho a publikoval svůj výzkum analýzy. Termín integrál sahá až k Johann Bernoulli.

V 19. století byla veškerá analýza postavena na pevnějších základech. V roce 1823 Augustin-Louis Cauchy poprvé vyvinul integrální termín, který splňuje dnešní požadavky na přísnost . Termíny Riemannova integrálu a Lebesgueova integrálu se objevily později . Konečně, vývoj teorie míry následoval na počátku 20. století.

Integrovaný pro kompaktní intervaly

„Kompaktní“ zde znamená omezené a uzavřené, takže se berou v úvahu pouze funkce v intervalech formuláře . Otevřené nebo neomezené intervaly nejsou povoleny. ${\ displaystyle [a, b]}$

motivace

Redukce složitých oblastí na integrály

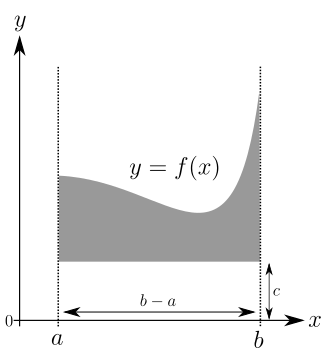
Jedním z cílů integrálního počtu je výpočet plochy křivočarě omezených oblastí roviny. Ve většině případů, které se v praxi vyskytují, jsou takové oblasti popsány dvěma spojitými funkcemi na kompaktním intervalu , jejichž grafy omezují oblast (levý obrázek). ${\ displaystyle f, g}$${\ displaystyle [a, b]}$

: :

Oblast šedé oblasti na levém obrázku se rovná rozdílu mezi šedými oblastmi na dvou pravých obrázcích. Stačí se tedy omezit na jednodušší případ oblasti ohraničené:

• graf funkce
• dvě svislé rovné čáry a${\ displaystyle x = a}$${\ displaystyle x = b}$
• stejně jako osa.${\ displaystyle x}$

Pro svůj zásadní význam má tento typ oblasti zvláštní název:

${\ Displaystyle \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x}$,

číst jako integrál až do asi${\ displaystyle a}$${\ displaystyle b}$ (nebo prostřednictvím ) z , . Dnes je tento faktor obecně používán jako čistá notační složka a znamená diferenciál na -osě. Místo výběru jiné proměnné kromě a například toho, co nemění hodnotu integrálu. ${\ displaystyle f}$${\ displaystyle x}$${\ displaystyle \ mathrm {d} x}$ ${\ displaystyle \ mathrm {d} x}$${\ displaystyle x}$${\ displaystyle x}$${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle t}$

Integrální negativní funkce

Pokud posunete graf funkce ve směru -osy o bit , do uvažované oblasti se přidá obdélník: ${\ displaystyle y}$${\ displaystyle c}$

:

Integrál se ve vzorcích mění podle plochy tohoto obdélníku šířky a výšky${\ Displaystyle ba}$${\ displaystyle c}$

${\ Displaystyle \ int _ {a} ^ {b} (f (x) + c) \, \ mathrm {d} x = \ int _ {a} ^ {b} f (x) \, \ mathrm {d } x + (ba) \ cdot c.}$

Pokud se podíváme na spojitou funkci, jejíž hodnoty jsou záporné, vždy můžeme najít a, takže hodnoty v intervalu jsou všechny kladné ( musí být větší než absolutní hodnota minima v ). S výše uvedenou úvahou člověk získá ${\ displaystyle c \ in \ mathbb {R}}$${\ displaystyle f (x) + c}$${\ displaystyle c}$${\ displaystyle f}$${\ displaystyle [a, b]}$

${\ Displaystyle \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x = \ int _ {a} ^ {b} (f (x) + c) \, \ mathrm {d } x- (ba) \ cdot c,}$

to znamená, že integrál je rozdíl mezi oblastmi bílé oblasti ve středu a okolním obdélníkem. Tento rozdíl je však záporný, to znamená, že pokud má být výše uvedený vzorec pro jakoukoli funkci správný, musí být oblasti pod osou počítány jako záporné. Mluví se tedy o orientované nebo směrované oblasti. ${\ displaystyle f}$${\ displaystyle x}$

Pokud je v intervalu, který má být zkoumán, jedna nebo více nul, integrál již neoznačuje oblast, ale součet (pozitivních) oblastí dílčích oblastí nad -osou a (negativních) oblastí dílčích oblastí níže aretačním kroužkem. Pokud potřebujete v takovém intervalu oblast mezi -osou a grafem funkce, integrál musí být rozdělen na nuly. ${\ displaystyle x}$${\ displaystyle x}$${\ displaystyle x}$

Cavalieriho princip a aditivita integrálu

Axiomatický přístup

Není snadné pojmout koncept oblasti matematicky přesným způsobem. V průběhu času k tomu byly vyvinuty různé koncepty. U většiny aplikací jsou však jejich detaily irelevantní, protože se mimo jiné shodují na třídě spojitých funkcí. V následujícím textu jsou uvedeny některé vlastnosti integrálu, které byly motivovány výše a které platí pro každý integrál bez ohledu na přesnou konstrukci. Kromě toho jasně definují integrál spojitých funkcí.

Nech to být reálná čísla a nechat to být vektorový prostor funkcí , která zahrnuje na spojité funkce . Funkce v se nazývají "integrovatelné". Pak je integrálem mapa ${\ displaystyle a <b}$ ${\ displaystyle {\ mathcal {F}}}$${\ Displaystyle [a, b] \ to \ mathbb {R}}$${\ displaystyle {\ mathcal {F}}}$

${\ displaystyle {\ mathcal {F}} \ to \ mathbb {R},}$

psaný

${\ Displaystyle f \ mapsto \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x,}$

s následujícími charakteristikami:

• Linearita: Pro funkce a platí ${\ displaystyle f, g \ in {\ mathcal {F}}}$${\ Displaystyle \ lambda \ in \ mathbb {R}}$
  • ${\ Displaystyle \ int _ {a} ^ {b} (f (x) + g (x)) \, \ mathrm {d} x = \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x + \ int _ {a} ^ {b} g (x) \, \ mathrm {d} x}$,
  • ${\ Displaystyle \ int _ {a} ^ {b} \ lambda f (x) \, \ mathrm {d} x = \ lambda \ cdot \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x}$.
• Monotónnost: Je pro každého , stejně tak je ${\ Displaystyle f (x) \ geq 0}$${\ Displaystyle x \ v [a, b]}$

  ${\ Displaystyle \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x \ geq 0.}$

• Integrál charakteristické funkce intervalu: je interval a je${\ Displaystyle I \ subseteq [a, b]}$

${\ Displaystyle \ chi _ {I} (x) = {\ begin {cases} 1 \, & \ mathrm {if} \ x \ in I \, \\ 0 \, & \ mathrm {if} \ x \ notin I \, \ end {cases}}}$

takže je

${\ Displaystyle \ int _ {a} ^ {b} \ chi _ {I} (x) \, \ mathrm {d} x}$

rovná délce intervalu .${\ displaystyle I}$

Označení

• Skutečná čísla a nazývají se integrační limity. Mohou být zapsány nad a pod integrální znak nebo na stranu integrálního znaku:${\ displaystyle a}$${\ displaystyle b}$

${\ displaystyle {\ textstyle \ int \ limits _ {a} ^ {b}} f (x) \, {\ rm {d}} x}$     nebo     ${\ Displaystyle \ int \ nolimits _ {a} ^ {b} f (x) \, {\ rm {d}} x}$

• Integrovaná funkce se nazývá integrand .${\ displaystyle f}$
• Proměnná se nazývá integrační proměnná . V případě integrace je proměnná, pak také mluví o integraci kolem . Integrační proměnná je zaměnitelná místo${\ displaystyle x}$${\ displaystyle x}$${\ displaystyle x}$

${\ Displaystyle \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x}$

můžete to udělat stejně dobře

${\ Displaystyle \ int _ {a} ^ {b} f (t) \, \ mathrm {d} t}$ nebo ${\ Displaystyle \ int _ {a} ^ {b} f (\ xi) \, \ mathrm {d} \ xi}$

psát. Ve výše uvedeném příkladu použití písmen nebo vede k nežádoucím nejasnostem, protože již fungují jako identifikátory integračních limitů. Měli byste proto zajistit, aby znaku použitému pro integrační proměnnou již nebyl přiřazen jiný význam.${\ displaystyle a}$${\ displaystyle b}$

• Složka „ “ se nazývá diferenciál , ale v tomto kontextu má většinou pouze symbolický význam. Proto zde není učiněn žádný pokus jej definovat. Integrační proměnnou lze vyčíst z diferenciálu.${\ displaystyle \ mathrm {d} x}$

Původ zápisu

Symbolická notace integrálů sahá k spolu-prvnímu popisovateli diferenciálního a integrálního počtu, Gottfriedu Wilhelmu Leibnizovi . Integrální znaménko ∫ je odvozen z dopisu dlouho s (y) pro Latinskou Summa . Multiplikativní zápis ukazuje, jak se integrál - po Riemannově integrálu - skládá z pruhů výšky a nekonečně malé šířky . ${\ Displaystyle f (x) \; \ mathrm {d} x}$${\ displaystyle f (x)}$${\ displaystyle \ mathrm {d} x}$

Alternativní pravopis ve fyzice

V teoretické fyzice se z pragmatických důvodů pro integrály často používá trochu odlišná notace (zejména pro vícenásobné integrály). Tam se koná

${\ Displaystyle \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x}$

často

${\ Displaystyle \ int _ {a} ^ {b} \ mathrm {d} xf (x)}$

někdy se obě hláskování používají na různých místech.

Druhý příklad má nevýhodu v tom, že funkce, které mají být integrovány ne a závorkách. Navíc může dojít k nedorozuměním , například s Lebesgueovým integrálem . Alternativní zápis má však také některé výhody: ${\ displaystyle f (x)}$${\ displaystyle \ textstyle \ int _ {a} ^ {b}}$${\ displaystyle \ mathrm {d} x}$

• Výraz zdůrazňuje, že integrál je lineární operátor, který působí na vše napravo od něj.${\ Displaystyle \ textstyle \ int _ {a} ^ {b} \ mathrm {d} x}$
• Integrály se často objevují ve fyzice, ve které má být integrovaná funkce dlouhá několik řádků nebo je integrována do několika neznámých . Pak už na začátku integrálu víte, které proměnné jsou integrovány a nad kterými limity se zápisem . Kromě toho je pak přiřazování proměnných k limitům jednodušší.${\ displaystyle x_ {1}, x_ {2}, \ dotsc, x_ {n}}$${\ Displaystyle \ textstyle \ int _ {a} ^ {b} \ mathrm {d} xf (x)}$
• Je zdůrazněna komutativita produktů v součtech vyskytujících se v Riemannově aproximaci .${\ Displaystyle \ Delta x_ {n} \ cdot f (x_ {n})}$

Příklad:

${\ Displaystyle \ int _ {a_ {1}} ^ {a_ {2}} \ mathrm {d} t \ int _ {b_ {1}} ^ {b_ {2}} \ mathrm {d} x_ {1} \ int _ {c_ {1}} ^ {c_ {2}} \ mathrm {d} x_ {2} \ int _ {d_ {1}} ^ {d_ {2}} \ mathrm {d} x_ {3} \, f (x_ {1}, x_ {2}, x_ {3}, t)}$

namísto

${\ Displaystyle \ int _ {a_ {1}} ^ {a_ {2}} \ int _ {b_ {1}} ^ {b_ {2}} \ int _ {c_ {1}} ^ {c_ {2} } \ int _ {d_ {1}} ^ {d_ {2}} f (x_ {1}, x_ {2}, x_ {3}, t) \, \ mathrm {d} x_ {3} \ mathrm { d} x_ {2} \ mathrm {d} x_ {1} \ mathrm {d} t}$

Jednoduché důsledky axiomů

• Je pro každého , stejně tak je${\ Displaystyle f (x) \ leq g (x)}$${\ Displaystyle a \ leq x \ leq b}$

${\ Displaystyle \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x \ leq \ int _ {a} ^ {b} g (x) \, \ mathrm {d} x. }$

• Jestliže jeden označuje na Supremum normu a na , pak platí následující${\ displaystyle \ | f \ | _ {\ infty}}$${\ displaystyle f}$${\ displaystyle [a, b]}$

${\ Displaystyle \ left | \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x \ right | \ leq (ba) \ cdot \ | f \ | _ {\ infty}.}$

• Je pro všechny s pevným číslem , pak platí${\ Displaystyle | f (x) -g (x) | <\ varepsilon}$${\ Displaystyle a \ leq x \ leq b}$${\ displaystyle \ varepsilon> 0}$

${\ Displaystyle \ left | \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x- \ int _ {a} ^ {b} g (x) \, \ mathrm {d} x \ vpravo | \ leq (ba) \ cdot \ varepsilon.}$

Z toho vyplývá: Pokud je posloupnost integrovatelných funkcí, která rovnoměrně konverguje k (integrovatelné) funkci , pak je ${\ displaystyle (f_ {n}) _ {n \ in \ mathbb {N}}}$${\ displaystyle f}$

${\ Displaystyle \ lim _ {n \ to \ infty} \ int _ {a} ^ {b} f_ {n} (x) \, \ mathrm {d} x = \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x.}$

Jinými slovy: integrál je spojitá funkce pro normu supremum.

• Integrály krok funkce: Je-li krok funkce , to znamená, že je disjunktní sjednocení intervalů délky , takže na je konstantní hodnotě , pak se použije${\ displaystyle f}$${\ displaystyle [a, b]}$${\ displaystyle I_ {k}}$${\ displaystyle L_ {k}}$${\ displaystyle f}$${\ displaystyle I_ {k}}$${\ displaystyle c_ {k}}$

${\ Displaystyle \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x = \ sum _ {k = 1} ^ {n} L_ {k} \ cdot c_ {k},}$

tedy jasně roven součtu orientovaných oblastí obdélníků mezi grafem funkce a osou.${\ displaystyle f}$${\ displaystyle x}$

Antiderivativa a hlavní věta diferenciálního a integrálního počtu

Integrace je nejednoznačné obrácení diferenciace. Aby to bylo přesnější, že koncepce je primitivní potřeby: Pokud je funkce, pak funkce se nazývá primitivní z v případě, že derivát z je roven : ${\ displaystyle f}$${\ displaystyle F}$${\ displaystyle f}$${\ displaystyle F}$${\ displaystyle f}$

${\ displaystyle F '= f}$

Tato inverze je nejednoznačná, protože různé funkce (např. Polynomické funkce, které se liší pouze v průsečíku osy Y) mohou mít jednu a tutéž derivaci, což znamená, že funkce nemá jen jednu, ale nekonečný počet antiderivativ.

Hlavní věta diferenciálního a integrálního počtu zakládá vztah mezi primitivní a integrálů. To říká: Je-li spojitá funkce na intervalu a je antiderivative , pak máme ${\ displaystyle f}$${\ displaystyle [a, b]}$${\ displaystyle F}$${\ displaystyle f}$

${\ Displaystyle \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x = F (b) -F (a).}$

Pravá strana je často zkrácena jako

${\ Displaystyle [F (x)] _ {a} ^ {b} = [F (x)] _ {x = a} ^ {x = b} = F (x) {\ Big |} _ {a} ^ {b} = F (x) {\ Big |} _ {x = a} ^ {x = b}}$ nebo podobné

psaný.

Tento vztah je hlavní metodou pro explicitní hodnocení integrálů. Obtíž obvykle spočívá v nalezení primitivní látky.

Pouhá existence je teoreticky zajištěna: integrální funkce

${\ Displaystyle x \ mapsto \ int _ {a} ^ {x} f (t) \, \ mathrm {d} t}$

je pro každého pomyslný . ${\ displaystyle a}$${\ displaystyle f}$

Vlastnosti antiderivativ

K antiderivativu můžete přidat konstantu a získat antiderivaci znovu: Pokud je primitiv k funkci a je konstanta, pak je ${\ displaystyle F}$${\ displaystyle f}$${\ displaystyle c \ in \ mathbb {R}}$

${\ Displaystyle (F + c) '= F \! \,' + 0 = F '= f.}$

Dvě antiderivativa stejné funkce definované v intervalu se liší konstantou: If a antiderivatives stejné funkce , pak je ${\ displaystyle F}$${\ displaystyle G}$${\ displaystyle f}$

${\ Displaystyle (FG) \! \, '= F'-G' = ff = 0,}$

rozdíl je tedy konstantní. V případě, že doména z definice je není interval, pak se rozdíl mezi dvěma primitivní je pouze lokálně konstantní . ${\ displaystyle FG}$${\ displaystyle f}$

Neurčitý integrál

Primitivní je také označována jako neurčitý integrál všech - ale někdy to také znamená, že soubor všech primitivní. Pokud je to pomyslný prvek, je často napsán nepřesně ${\ displaystyle f (x)}$${\ displaystyle F (x)}$

${\ Displaystyle \ int f (x) \, \ mathrm {d} x = F (x) + C,}$

k označení, že každý primitivní prvek má formu s konstantou . Konstanta se nazývá konstanta integrace.${\ displaystyle f}$${\ displaystyle F (x) + C}$${\ displaystyle C}$${\ displaystyle C}$

Všimněte si toho zápisu

${\ Displaystyle \ int f (x) \, \ mathrm {d} x}$

ve vzorcích se však také často používá k označení, že rovnice platí pro libovolné, důsledně zvolené limity; například je s

${\ Displaystyle \ int cf (x) \, \ mathrm {d} x = c \ int f (x) \, \ mathrm {d} x}$

znamenalo, že

${\ Displaystyle \ int _ {a} ^ {b} cf (x) \, \ mathrm {d} x = c \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x}$

platí pro jakékoli . ${\ displaystyle a, b}$

Stanovení antiderivativ

Viz článek: Tabulka derivačních a antiderivativních nebo neurčitých integrálů ve sbírce matematických vzorců .

Na rozdíl od derivační funkce je explicitní výpočet primitivní funkce pro mnoho funkcí velmi obtížný nebo nemožný. Proto jsou integrály často vyhledávány v tabulkách (např. Integrální tabulka ). Pro ruční výpočet antiderivace je často užitečné šikovně použít následující standardní techniky.

Částečná integrace

Částečná integrace je opakem součinového pravidla diferenciálního počtu. To je:

${\ Displaystyle \ int _ {a} ^ {b} f '(x) \ cdot g (x) \, \ mathrm {d} x = [f (x) \ cdot g (x)] _ {a} ^ {b} - \ int _ {a} ^ {b} f (x) \ cdot g '(x) \, \ mathrm {d} x}$

Toto pravidlo je užitečné, když je funkce integrovatelnější než funkce . Zde je však třeba posoudit produkty a nikoli samotné faktory. ${\ Displaystyle f (x) \ cdot g '(x)}$${\ Displaystyle f '(x) \ cdot g (x)}$

Příklad:

${\ Displaystyle \ int _ {a} ^ {b} x \ ln (x) \, \ mathrm {d} x}$

Pokud nastavíte

${\ Displaystyle f '(x) = x \,}$ a ${\ Displaystyle g (x) = \ ln (x) \,}$

takže je

${\ Displaystyle f (x) = {\ frac {x ^ {2}} {2}}}$ a ${\ Displaystyle g '(x) = {\ frac {1} {x}}}$

a dostanete

${\ Displaystyle {\ begin {aligned} \ int _ {a} ^ {b} x \ ln (x) \, \ mathrm {d} x & = {\ frac {b ^ {2}} {2}} \ ln (b) - {\ frac {a ^ {2}} {2}} \ ln (a) - \ int _ {a} ^ {b} {\ frac {x ^ {2}} {2}} \ cdot {\ frac {1} {x}} \, \ mathrm {d} x \\ & = {\ frac {b ^ {2}} {2}} \ left (\ ln (b) - {\ frac { 1} {2}} \ right) - {\ frac {a ^ {2}} {2}} \ left (\ ln (a) - {\ frac {1} {2}} \ right). \ End { zarovnáno}}}$

Integrace prostřednictvím substituce

Substituční pravidlo je důležitým nástrojem pro výpočet některých obtížných integrálů, protože umožňuje integrovat určité změny funkce při změně integračních limitů. Je to protějšek řetězového pravidla v diferenciálním počtu.

Nechť se a být antiderivative , pak je antiderivative , protože je držitelem ${\ Displaystyle \ varphi (x) = f (g (x)) \ cdot g '(x)}$${\ displaystyle g '\ neq 0}$${\ displaystyle F}$${\ displaystyle f}$${\ Displaystyle \ Phi (x) = F (g (x))}$${\ Displaystyle \ varphi}$

${\ displaystyle {\ frac {\ varphi (x)} {g '(x)}} = f (g (x))}$

a se střídáním

${\ Displaystyle z = g (x), \ quad \ mathrm {d} z = g '(x) \ mathrm {d} x}$

na konci

${\ Displaystyle {\ begin {aligned} \ int _ {a} ^ {b} f (g (x)) g '(x) \ mathrm {d} x & = \ int _ {g (a)} ^ { g (b)} f (z) \ mathrm {d} z \\ & = F (g (b)) - F (g (a)) \\ & = \ Phi (b) - \ Phi (a). \ end {aligned}}}$

Přetváření částečným rozkladem frakce

V případě frakčně-racionálních funkcí vede polynomické dělení nebo částečný rozklad často k transformaci funkce, která umožňuje uplatnění jednoho z integračních pravidel.

Speciální postupy

Antiderivativum je často možné určit pomocí speciální formy integrandu.

Další možností je začít se známým integrálem a transformovat jej pomocí integračních technik, dokud není získán požadovaný integrál. Příklad:

Abychom určili, částečně integrujeme následující podobný integrál: ${\ Displaystyle \ textstyle \ int {\ frac {\ mathrm {d} x} {(1 + x ^ {2}) ^ {2}}}}$

${\ Displaystyle {\ begin {aligned} \ arctan x & = \ int 1 \ cdot {\ frac {1} {1 + x ^ {2}}} \, \ mathrm {d} x \\ & = x \ cdot {\ frac {1} {1 + x ^ {2}}} + \ int x \ cdot {\ frac {2x} {(1 + x ^ {2}) ^ {2}}} \, \ mathrm {d } x \\ & = {\ frac {x} {1 + x ^ {2}}} + \ int \ left ({\ frac {2x ^ {2}} {(1 + x ^ {2}) ^ { 2}}} + {\ frac {2} {(1 + x ^ {2}) ^ {2}}} \ right) \, \ mathrm {d} x- \ int {\ frac {2} {(1 + x ^ {2}) ^ {2}}} \, \ mathrm {d} x \\ & = {\ frac {x} {1 + x ^ {2}}} + 2 \ int {\ frac {1 + x ^ {2}} {(1 + x ^ {2}) ^ {2}}} \, \ mathrm {d} x-2 \ int {\ frac {1} {(1 + x ^ {2} ) ^ {2}}} \, \ mathrm {d} x \\ & = {\ frac {x} {1 + x ^ {2}}} + 2 \ arctan x-2 \ int {\ frac {\ mathrm {d} x} {(1 + x ^ {2}) ^ {2}}} \ end {zarovnáno}}}$

Změnou to následuje

${\ Displaystyle \ int {\ frac {\ mathrm {d} x} {(1 + x ^ {2}) ^ {2}}} = {\ frac {1} {2}} \ left ({\ frac { x} {1 + x ^ {2}}} + \ arctan x \ right).}$

Vícenásobná integrace

Pokud má být funkce integrována vícekrát, Cauchyův vzorec pro vícenásobnou integraci poskytuje v bodě iterovaný integrál${\ displaystyle f}$${\ displaystyle n}$${\ displaystyle f}$${\ displaystyle x}$

${\ Displaystyle I ^ {n} (x) = \ int _ {a} ^ {x} \ int _ {a} ^ {\ sigma _ {1}} \ cdots \ int _ {a} ^ {\ sigma _ {n-1}} f (\ sigma _ {n}) \, \ mathrm {d} \ sigma _ {n} \ cdots \, \ mathrm {d} \ sigma _ {2} \, \ mathrm {d} \ sigma _ {1}}$

následující integrál:

${\ Displaystyle I ^ {n} (x) = {\ frac {1} {(n-1)!}} \ int _ {a} ^ {x} \ left (xt \ right) ^ {n-1} f (t) \, \ mathrm {d} t}$.

Aplikace

Střední hodnoty spojitých funkcí

Pro výpočet střední hodnoty dané spojité funkce v intervalu se používá vzorec ${\ displaystyle m}$ ${\ displaystyle f}$ ${\ displaystyle [a, b]}$

${\ Displaystyle m = {\ frac {1} {ba}} \ int _ {a} ^ {b} f (x) \ mathrm {d} x.}$

Protože tato definice pro funkce schodiště odpovídá obvyklému pojmu střední hodnoty, je toto zobecnění užitečné.

Hodnota věta integrálního počtu střední říká, že tato střední hodnota je ve skutečnosti předpokládá kontinuální funkce v intervalu . ${\ displaystyle [a, b]}$

Příklad pojmu integrál ve fyzice

Fyzický jev , který lze použít k vysvětlení pojmu integrálu je volný pád z těla ve v zemském gravitačním poli . Zrychlení z volného pádu ve střední Evropě je cca. 9,81 m / s². Rychlost těla v době, proto může být vyjádřen vzorcem ${\ displaystyle g}$ ${\ displaystyle v}$${\ displaystyle t}$

${\ Displaystyle v = g \ cdot t}$

vyjádřit.

Nyní by však měla být vypočítána vzdálenost , kterou padající tělo urazí za určitý čas . Problém je v tom, že rychlost těla se v průběhu času zvyšuje. K vyřešení problému se předpokládá, že po krátkou dobu rychlost , která vyplývá z času , zůstává konstantní. ${\ Displaystyle l}$${\ displaystyle T}$${\ displaystyle v}$${\ Displaystyle \ Delta t}$${\ displaystyle v}$${\ Displaystyle g \ cdot t}$

Nárůst ujeté vzdálenosti za krátkou dobu proto je ${\ Displaystyle \ Delta t}$

${\ Displaystyle \ Delta l = g \ cdot t \, \ cdot \ Delta t}$.

Celou vzdálenost lze tedy popsat jako

${\ Displaystyle l = \ sum \ left (g \ cdot t \, \ cdot \ Delta t \ right)}$

vyjádřit. Pokud nyní necháte časový rozdíl směřovat k nule, dostanete ${\ Displaystyle \ Delta t}$

${\ Displaystyle l = \ lim _ {\ Delta t \ to 0} \ left (\ sum \ left (g \ cdot t \, \ cdot \ Delta t \ right) \ right) = \ int _ {0} ^ { T} \ left (g \ cdot t \; \ mathrm {d} t \, \ right).}$

Integrál lze analyticky zadat pomocí

${\ Displaystyle l = \, {\ frac {g} {2}} \ cdot T ^ {2}.}$

Obecné řešení vede k pohybové rovnici těla spadajícího do konstantního gravitačního pole:

${\ Displaystyle l = {\ frac {g} {2}} \ cdot t ^ {2}}$

Dále z této pohybové rovnice, rozlišením podle času, může být rychlostní rovnice:

${\ Displaystyle v = g \ cdot t}$

a odvodit opětovným rozlišením zrychlení:

${\ displaystyle a = g}$

Dalšími jednoduchými příklady jsou:

• Energie je integrál výkonu v průběhu času.
• Elektrický náboj na kondenzátoru je integrál proudu protékajícího něj v průběhu času.
• Integrál součinu spektrální ozáření ( E _e (ν) ve W / m ² Hz ) se spektrální křivkou citlivosti na světlo oka poskytuje osvětlenost ( E v luxech = lumen / m ² ).
• Integrál rychlosti proudění (podélná složka) v průřezu potrubí zajišťuje celý objemový průtok potrubím (další vícerozměrné integrály viz níže ).

Stavby

Cauchyův integrál

Kontrolní funkce je funkce, která může být aproximována rovnoměrně pomocí krok funkcí . Vzhledem k výše uvedené kompatibilitě integrálu s jednotnými limity je pro řídicí funkci, která je jednotným limitem posloupnosti krokových funkcí, integrál definován jako ${\ displaystyle f}$${\ displaystyle t_ {n}}$

${\ Displaystyle \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x = \ lim _ {n \ to \ infty} \ int _ {a} ^ {b} t_ {n} (x) \, \ mathrm {d} x,}$

kde integrál pro krokové funkce je definován výše uvedeným vzorcem.

Třída řídicích funkcí zahrnuje všechny spojité funkce a všechny monotónní funkce , jakož i všechny funkce, pro které mohou být rozděleny do konečně mnoha intervalech , takže omezení z na kontinuálním nebo monotónní funkce je na uzavřeném intervalu , tj. H. všechny kusové spojité funkce. Obsahuje také funkce omezené variace , protože takovou funkci lze znázornit jako rozdíl mezi dvěma monotónně rostoucími funkcemi. Pro mnoho praktických účelů je tato integrální konstrukce zcela dostačující. ${\ displaystyle f}$${\ displaystyle [a, b]}$${\ displaystyle I_ {k}}$${\ displaystyle f}$${\ displaystyle I_ {k}}$${\ displaystyle {\ bar {I}} _ {k}}$

Existují také spojité funkce s nekonečnou variací, jako je B. funkce definovaná intervalem a pro interval (viz variace ). ${\ displaystyle 0 \ mapsto 0}$${\ displaystyle t \ mapsto t \ cos {\ tfrac {\ pi / 2} {t}}}$${\ Displaystyle 0 <t \ leq 1}$${\ Displaystyle [0,1]}$

Riemannův integrál

Jeden přístup k výpočtu integrálu podle Riemanna je aproximace funkce, která má být integrována funkcí kroku ; nikoli však jednotnou aproximací samotné funkce, ale aproximací plochy pomocí obdélníkových součtů.

Plocha je aproximována součtem ploch jednotlivých obdélníků pod jednotlivými „kroky“. Pro každé rozdělení integračního intervalu můžete jako úroveň úrovně zvolit libovolnou funkční hodnotu v každém dílčím intervalu.

Ty jsou poté, co německý matematik Bernhard Riemann nazval Riemannovy součty. Pokud si člověk zvolí supremum funkce jako výšku obdélníku v každém dílčím intervalu rozkladu , pak vznikne horní součet, s infimem nižší součet.

Riemannův integrál lze definovat pomocí horních a dolních součtů, viz Riemannův integrál. Pokud horní a dolní součet konvergují ke stejné mezní hodnotě , pak je tato mezní hodnota integrálem v Riemannově smyslu. V tomto smyslu lze integrovat z. B. všechny funkce, pro které Cauchyův integrál existuje.

Riemannův integrál existuje např. B. ne pro indikátorovou funkci racionálních čísel v intervalu , tj. H. pro funkci Dirichlet . Proto rozšířené integrální termíny zavedli Henri Léon Lebesgue ( Lebesgueův integrál ), Thomas Jean Stieltjes ( Stieltjesův integrál ) a Alfréd Haar , které reprodukují Riemannův integrál pro spojité integrandy. ${\ Displaystyle [0,1]}$

Stieltjesův integrál

Stieltjesův integrál je založen na monotónních funkcích nebo na funkcích s konečnou variací , tj. Na rozdílech mezi dvěma monotónními funkcemi a součty Riemann-Stieltjes jsou pro spojité funkce definovány jako ${\ displaystyle g (x)}$${\ displaystyle f}$

${\ Displaystyle \ sum _ {i = 0} ^ {n -1} \, f (x_ {i}) \, \ {g (x_ {i + 1}) - g (x_ {i}) \}. }$

Takzvaný Riemann-Stieltjesův integrál se pak získá vytvořením limitu obvyklým způsobem . ${\ Displaystyle \ textstyle \ int _ {I} \, f \, \ mathrm {d} g}$

Takové integrály jsou také definovány, pokud funkce není odlišitelná (jinak platí ). Známým protipříkladem je takzvaná Heavisideova funkce , jejíž hodnota je nulová pro záporná čísla, jedna pro kladná a z. B. k věci . Člověk píše pro a tak přijímá „zobecněnou funkci“ , takzvanou Diracovu míru , jako míru, která je definována pouze pro daný bod . ${\ displaystyle g}$${\ Displaystyle \ mathrm {d} g \ equiv g '(x) \, \ mathrm {d} x}$ ${\ displaystyle \ Theta (x)}$${\ displaystyle x}$${\ displaystyle = 1/2}$${\ displaystyle x = 0}$${\ displaystyle g (x) = \ Theta (x),}$ ${\ Displaystyle \ mathrm {d} g = \ delta (x) \ mathrm {d} x}$ ${\ displaystyle \ delta (x)}$${\ displaystyle x = 0}$

Lebesgueův integrál

Lebesgueův integrál poskytuje modernější a - v mnoha ohledech - lepší integrální termín než Riemannův integrál. Například umožňuje integraci pomocí obecných dimenzionálních prostorů . To znamená, že množství, mohou být přiřazeny k opatření, která nemusí nutně odpovídat jejich geometrické délky nebo objemu, jako je pravděpodobnost opatření v teorii pravděpodobnosti . Míra, která odpovídá intuitivnímu pojmu délky nebo objemu, je Lebesgueova míra . Integrál v této dimenzi se zpravidla označuje jako Lebesgueův integrál . Lze dokázat, že pro každou Riemannovu funkci integrovatelnou v kompaktním intervalu existuje také odpovídající Lebesgueův integrál a hodnoty obou integrálů souhlasí. Naopak, ne všechny Lebesgueovy integrovatelné funkce jsou také Riemann-integrovatelné. Nejznámějším příkladem je Dirichletova funkce , tj. Funkce, která má pro racionální čísla hodnotu jedna, ale pro iracionální čísla hodnotu nula. Kromě větší třídy integrovatelných funkcí se Lebesgueův integrál odlišuje od Riemannova integrálu především lepšími konvergenčními teorémy ( věta o monotónní konvergenci , větou o majorizované konvergenci ) a lepšími vlastnostmi funkčních prostorů normalizovaných Lebesgueovým integrálem ( přibližně úplnost ).

V moderní matematice je integrální nebo integrační teorie často chápána jako Lebesgueův integrální termín.

Nesprávný integrál

Riemannův integrál je (v jednorozměrném prostoru) definován pouze pro kompaktní , tj. Omezené a uzavřené intervaly. Nesprávný integrál nabízí zobecnění neomezených domén definice nebo funkcí se singularitami . I v Lebesgueově teorii lze uvažovat o nevhodných integrálech, ale není to tak produktivní, protože Lebesgueův integrál již může integrovat mnoho funkcí se singularitami nebo neomezenou doménou.

Metoda výpočtu určitých a nevhodných integrálů

Numerické metody

Je často obtížné nebo nemožné explicitně specifikovat antiderivativum. V mnoha případech však stačí přibližně vypočítat konkrétní integrál. Člověk pak mluví o numerické kvadratuře nebo numerické integraci . Mnoho metod pro numerickou kvadraturu je založeno na aproximaci funkce funkcemi, které jsou snadněji integrovatelné, například polynomy. Lichoběžníkové pravidlo nebo Simpsonova vzorce (zvláštní případ, který je známý jako Keplerova hlaveň pravidla ) jsou příklady toho, okud interpolační polynom je umístěn prostřednictvím funkce a integrovány.

Dlouho před rozšířením počítačů byly vyvinuty metody pro automatické řízení velikosti kroku pro numerickou integraci . Počítačová algebra dnes nabízí možnost řešení komplexních integrálů numericky ve stále kratších časech nebo se stále přesnějšími řešeními, přičemž i u výkonných systémů stále existují potíže s nevhodnými integrály, pro jejichž výpočet mají často speciální metody jako Gauss-Kronrod být použit. Příkladem takového tvrdého integrálu je:

${\ Displaystyle \ int _ {0} ^ {\ infty} {\ frac {\ ln (1 + x)} {\ ln ^ {2} x + \ pi ^ {2}}} \ cdot {\ frac {\ mathrm {d} x} {x ^ {2}}} = \ gamma}$

Klasickými metodami jsou např. B. Eulerův empirický vzorec , ve kterém je určitý integrál aproximován obecně asymptotickou řadou . Další metody vycházejí z teorie rozdílového počtu , důležitým příkladem je zde Gregoryho integrační vzorec.

Přesné postupy

Existuje řada metod, pomocí kterých lze přesně a symbolicky vypočítat určité a nevhodné integrály.

Pokud je znám spojitý a kladný činitel , může být určitý integrál ${\ displaystyle f}$${\ displaystyle f}$${\ displaystyle F}$

${\ Displaystyle \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x = F (b) -F (a)}$

vypočítat podle hlavní klauzule. Problém je v tom, že provoz neurčité integrace vede k rozšíření daných funkčních tříd. Například integrace racionálních funkcí v rámci třídy není úplná a vede k funkcím a . Není uzavřena ani třída takzvaných elementárních funkcí . Tak Joseph Liouville dokázal, že funkce nemá elementární antiderivative. Leonhard Euler byl jedním z prvních, kdo vyvinul metody pro přesný výpočet určitých a nevhodných integrálů bez určení antiderivativu. Postupem času se objevilo mnoho obecnějších a konkrétnějších metod specifické integrace: ${\ displaystyle \ ln}$${\ Displaystyle \ arctan}$${\ displaystyle e ^ {- x ^ {2}}}$

• Pomocí zbytkové věty
• Reprezentace integrálu v závislosti na parametru pomocí speciálních funkcí
• Diferenciace nebo integrace integrálu podle parametru a záměna hraničních procesů
• Použití sériového rozšíření integrandu s integrací podle termínu
• snížit integrál k sobě nebo k jinému částečnou integrací a substitucí

Do konce 20. století byly vytvořeny četné (někdy vícesvazkové) integrální tabulky s určitými integrály. Několik příkladů pro ilustraci problému:

${\ Displaystyle \ int _ {0} ^ {1} {\ frac {\ ln (1 + x)} {x ^ {2} +1}} \, \ mathrm {d} x = {\ frac {\ pi } {8}} \ ln 2}$

${\ Displaystyle \ int _ {0} ^ {\ pi} \ ln \ sin x \, \ mathrm {d} x = - \ pi \ ln 2}$

Speciální integrály

Existuje řada určitých a nevhodných integrálů, které mají pro matematiku určitý význam, a proto mají své vlastní jméno:

• Eulerovy integrály prvního a druhého druhu
• Gaussova chyba integrál

${\ Displaystyle \ int _ {- \ infty} ^ {\ infty} e ^ {- t ^ {2}} \, \ mathrm {d} t = {\ sqrt {\ pi}}}$

• Fresnelovy integrály

${\ Displaystyle \ int _ {0} ^ {\ infty} \ cos t ^ {2} \, \ mathrm {d} t = \ int _ {0} ^ {\ infty} \ sin t ^ {2} \, \ mathrm {d} t = {\ tfrac {1} {4}} {\ sqrt {2 \ pi}}}$

• Raabeho integrál

${\ Displaystyle \ int \ limits _ {a} ^ {a + 1} \ log \ Gamma (t) \, \ mathrm {d} t = {\ tfrac {1} {2}} \ log 2 \ pi + a \ log aa, \ quad a \ geq 0,}$   a zejména pro a  :${\ displaystyle a = 0}$${\ displaystyle a = e}$${\ Displaystyle \ int _ {0} ^ {1} \ log \ Gamma (t) \, \ mathrm {d} t = {\ tfrac {1} {2}} \ log 2 \ pi}$

• Frullanské integrály

${\ Displaystyle \ int _ {0} ^ {\ infty} {\ frac {f (ax) -f (bx)} {x}} \, \ mathrm {d} x}$

Vícerozměrná integrace

Integrály cesty

Integrály skutečné cesty a délka křivky

Pokud je cesta , tj. Kontinuální mapování, a skalární funkce, pak je cesta integrál ze spolu je definován jako ${\ Displaystyle \ gamma \ colon [a, b] \ to \ mathbb {R} ^ {n}}$${\ Displaystyle f \ colon \ mathbb {R} ^ {n} \ to \ mathbb {R}}$${\ displaystyle f}$${\ displaystyle \ gamma}$

${\ Displaystyle \ int _ {\ gamma} f (x) \, \ mathrm {d} x = \ int _ {a} ^ {b} f (\ gamma (t)) \, \ | {\ dot {\ gamma}} (t) \ | \, \ mathrm {d} t.}$

Pokud z výše uvedeného vzorce dostaneme délku křivky (fyzicky řečeno) jako integrál rychlosti v čase: ${\ Displaystyle f \ equiv 1}$${\ Displaystyle \ gamma \ colon [a, b] \ to \ mathbb {R} ^ {2}}$

${\ Displaystyle L (\ gamma) = \ int _ {a} ^ {b} \ | {\ dot {\ gamma}} (t) \ | \, \ mathrm {d} t = \ int _ {a} ^ {b} {\ sqrt {{\ dot {x}} (t) ^ {2} + {\ dot {y}} (t) ^ {2}}} \, \ mathrm {d} t}$

Integrály skutečné cesty pro vektorové funkce

Ve fyzice se často používají integrály cesty následující formy: je vektorová funkce a stává se integrálem ${\ displaystyle {\ vec {f}}}$${\ Displaystyle \ mathbb {R} ^ {n} \ to \ mathbb {R} ^ {n}}$

${\ Displaystyle \ int _ {\ gamma} {\ vec {f}} (x) \ cdot \ mathrm {d} x = \ int _ {a} ^ {b} \ langle {\ vec {f}} (\ gamma (t)), {\ dot {\ gamma}} (t) \ rangle \, \ mathrm {d} t}$

kde výraz v lomených závorkách je skalární součin .

Integrály komplexní cesty

V teorii funkcí , tj. Rozšíření analýzy o funkce komplexní proměnné, již nestačí specifikovat dolní a horní meze integrace. Na rozdíl od dvou bodů na číselné ose mohou být dva body na komplexní rovině navzájem spojeny mnoha způsoby. Proto určitý integrál v teorii funkcí je v podstatě integrál cesty . Zbytková věta platí pro uzavřené cesty , důležitý výsledek Cauchyho: Integrál meromorfní funkce podél uzavřené cesty závisí výhradně na počtu uzavřených singularit. Pokud v oblasti integrace neexistují žádné singularity, je nula.

Povrchové integrály

Příklad: Výpočet obsahu místnosti

Jako příklad se objem mezi grafem funkce vypočítá s přes čtvereček jednotky . Za tímto účelem rozdělíte integrál na dva integrály, jeden pro - a druhý pro - souřadnici: ${\ Displaystyle f \ colon \ mathbb {R} ^ {2} \ to \ mathbb {R}}$${\ Displaystyle f (x, y): = x ^ {2} + y}$ ${\ Displaystyle I: = [0,1] \ krát [0,1]}$${\ displaystyle I}$${\ displaystyle x}$${\ displaystyle y}$

${\ Displaystyle {\ begin {aligned} \ int _ {[0,1] \ times [0,1]} f (x, y) \, \ mathrm {d} (x, y) & = \ int _ { 0} ^ {1} \ int _ {0} ^ {1} f (x, y) \, \ mathrm {d} x \, \ mathrm {d} y = \ int _ {0} ^ {1} \ int _ {0} ^ {1} (x ^ {2} + y) \, \ mathrm {d} x \, \ mathrm {d} y \\ & = \ int _ {0} ^ {1} \ left [{\ tfrac {1} {3}} x ^ {3} + yx \ right] _ {x = 0} ^ {1} \, \ mathrm {d} y = \ int _ {0} ^ {1} \ left ({\ tfrac {1} {3}} + y \ right) \ mathrm {d} y = \ left [{\ tfrac {1} {3}} y + {\ tfrac {1} {2}} y ^ {2} \ right] _ {y = 0} ^ {1} = {\ tfrac {5} {6}} \ end {aligned}}}$

Pro povrchový integrál udává plochu integračního povrchu. ${\ Displaystyle f \ equiv 1}$

Integrály objemu

Pro objemový integrál vypočítá objemový obsah integrační oblasti. ${\ Displaystyle f \ equiv 1}$

Integrace napříč vícerozměrnými a vyššími oblastmi

Koncept integrálu lze zobecnit na případ, že nosná množina, na které integrand funguje, není číselná řada , ale -dimenzionální euklidovský prostor . ${\ displaystyle f}$${\ displaystyle \ mathbb {R}}$${\ displaystyle n}$ ${\ displaystyle \ mathbb {R} ^ {n}}$

Fubiniho věta a transformační věta

Pro vícerozměrné integrály, tj. Také plošné a objemové integrály, se používá Fubiniho věta , která umožňuje rozdělení integrálů na jednotlivé souřadnice v libovolném pořadí a jejich zpracování jeden po druhém:

${\ Displaystyle {\ begin {aligned} \ int _ {V} f \ left ({\ vec {r}} \ right) \ mathrm {d} ^ {3} r & = \ iiint f (x, y, z ) \ mathrm {d} z \, \ mathrm {d} y \, \ mathrm {d} x \\ & = \ int \ left (\ int \ left (\ int f (x, y, z) \ mathrm { d} z \ right) \ mathrm {d} y \ right) \ mathrm {d} x \ end {zarovnaný}}}$

Integrační meze jednorozměrné integrálů v , a musí být stanovena z omezení objemu . Analogicky k nevhodným integrálům v jednorozměrném (viz výše) lze také uvažovat integrály v celém neomezeném -dimenzionálním prostoru. ${\ displaystyle x}$${\ displaystyle y}$${\ Displaystyle z}$${\ displaystyle V}$${\ displaystyle n}$

Zobecnění pravidla substituce ve vícerozměrné je transformační věta . Být otevřený a injective , nepřetržitě differentiable mapování, za jejichž funkční determinant platí pro všechny . Pak ${\ displaystyle \ Omega \ subset \ mathbb {R} ^ {d}}$ ${\ Displaystyle \ Phi \ colon \ Omega \ to \ mathbb {R} ^ {d}}$ ${\ Displaystyle \ det (D \ Phi (x)) \ neq 0}$${\ displaystyle x \ in \ Omega}$

${\ Displaystyle \ int _ {\ Phi (\ Omega)} f (y) \, \ mathrm {d} y = \ int _ {\ Omega} f (\ Phi (x)) \ left | \ det (D \ Phi (x)) \ right | \ mathrm {d} x.}$

Integrály přes rozdělovače

Integrace na povrchu oblasti je zvláště zajímavá v mnoha fyzických aplikacích. Takové povrchy jsou obvykle popsány pomocí sběrných potrubí . Ty jsou popsány takzvanými mapami.

Integrace přes oblast mapy

Nechť je -rozměrný podrozměr a mapová oblast v , tj. Otevřená podmnožina v , pro kterou existuje mapa, která ji mapuje diffeomorfně na otevřenou podmnožinu . Dále nechme parametrizaci , tj. Spojitě diferencovatelné mapování, jehož derivace má plnou hodnost, která se mapuje homeomorfně na . Pak je integrál funkce v oblasti mapy definován následovně: ${\ displaystyle M}$${\ displaystyle d}$${\ displaystyle \ mathbb {R} ^ {n}}$${\ displaystyle U}$${\ displaystyle M}$${\ displaystyle M}$${\ Displaystyle \ mathbb {R} ^ {d}}$${\ displaystyle \ gamma \ colon \ Omega \ to U}$${\ displaystyle U}$${\ displaystyle \ Omega}$ ${\ displaystyle \ gamma (\ Omega)}$${\ displaystyle U}$

${\ Displaystyle \ int _ {U} f \ mathrm {d} s: = \ int _ {\ Omega} f (\ gamma (u)) {\ sqrt {g ^ {\ gamma} (u)}} \ mathrm {d} u,}$

kde je na Gramův determinant . Správný integrál lze vypočítat pomocí výše popsaných metod vícerozměrné integrace. Rovnost v podstatě vyplývá z transformační věty. ${\ Displaystyle g ^ {\ gamma} (u) = \ det ((\ gamma '(u)) ^ {\ mathsf {T}} \ cdot \ gamma' (u))}$

Integrace přes dílčí potrubí

Pokud existuje rozpis 1, který je kompatibilní s mapami dílčího rozdělovače, lze jej jednoduše integrovat a sčítat samostatně přes oblasti mapy.

Gaussova integrální věta a Stokesova věta

U speciálních funkcí lze integrály vypočítat jednodušeji pomocí dílčích rozdělovačů. Ve fyzice jsou zvláště důležitá dvě tvrzení:

Na jedné straně existuje Gaussova integrální věta , podle které je objemový integrál přes divergenci vektorového pole roven povrchovému integrálu nad vektorovým polem ( tok pole povrchem): Buďte kompaktní s hladkým hrana v sekcích . Nechte hranu orientovat vnějším normálním jednotkovým polem . Dále nechť je průběžně diferencovatelné vektorové pole na otevřené sousedství . Pak platí ${\ Displaystyle V \ subset \ mathbb {R} ^ {n}}$ ${\ displaystyle \ partial V}$${\ displaystyle {\ vec {n}}}$${\ displaystyle {\ vec {F}}}$${\ displaystyle V}$

${\ Displaystyle \ int _ {V} \ jméno operátora {div} {\ vec {F}} \, \ mathrm {d} ^ {(n)} V = \ mast _ {\ částečný V} {\ vec {F} } \ cdot \ mathrm {d} ^ {(n-1)} {\ vec {S}}}$

se zkratkou . ${\ Displaystyle \ mathrm {d} ^ {(n-1)} {\ vec {S}} = {\ vec {n}} \, \ mathrm {d} ^ {(n-1)} S}$

Tato věta interpretuje divergenci jako takzvanou zdrojovou hustotu vektorového pole. Rozměr příslušného integračního potrubí je navíc zdůrazněna pomocí indexů nebo na operátora. ${\ displaystyle (n)}$${\ Displaystyle (n-1)}$${\ displaystyle \ mathrm {d}}$

Pokud se explicitně (bez indexování) používá více integrálů pro : ${\ displaystyle n = 3}$

${\ displaystyle \ iiint _ {V} \ operatorname {div} \, {\ vec {F}} ({\ vec {x}}) \, \ mathrm {d} V = \ iint _ {\ částečný V} { \ vec {F}} \ cdot \ mathrm {d} {\ vec {S}}}$

Takže: Integrál divergence v celém objemu se rovná integrálu toku z povrchu.

Za druhé, Stokesovu větu , která je vyjádřením diferenciální geometrie a ve zvláštním případě trojrozměrného prostoru lze psát přímo s více integrály.

Pokud existuje dvourozměrný dílčí potrubí trojrozměrného euklidovského prostoru , pak platí ${\ displaystyle M}$ ${\ displaystyle \ mathbb {R} ^ {3}}$

${\ displaystyle \ iint _ {M} \ operatorname {rot} {\ vec {F}} \ cdot \ mathrm {d} {\ vec {S}} = \ int _ {\ partial M} {\ vec {F} } \ cdot \ mathrm {d} {\ vec {r}},}$

kde znamená na otáčení vektorového pole . ${\ displaystyle \ operatorname {red} {\ vec {F}}}$${\ displaystyle {\ vec {F}}}$

Tato věta interpretuje rotaci vektorového pole jako takzvanou vírovou hustotu vektorového pole; kde vektor třísložková a hrana z uzavřené křivky im . ${\ displaystyle \ mathrm {d} {\ vec {r}}}$${\ Displaystyle (\ mathrm {d} x, \ mathrm {d} y, \ mathrm {d} z)}$${\ displaystyle \ partial M}$${\ displaystyle M}$${\ displaystyle \ mathbb {R} ^ {3}}$

Integrace vektorových funkcí

Integrace funkcí, které nejsou skutečné nebo komplexní, ale nabývají hodnot v obecnějším vektorovém prostoru, je také možné mnoha různými způsoby.

Přímou generalizací Lebesgueova integrálu na Banachovy prostorově hodnotné funkce je Bochnerův integrál (po Salomonu Bochnerovi ). Mnoho výsledků jednorozměrné teorie je doslova přeneseno do Banachových prostor.

Přenos definice Riemannova integrálu na funkce s vektorovou hodnotou pomocí Riemannových součtů také není obtížné. Zásadním rozdílem zde však je, že ne každá Riemannova integrovatelná funkce pak může být Bochnerově integrovatelná. ${\ Displaystyle f \ colon [a, b] \ až V}$

Společnou generalizací Bochnerova a Riemannovského integrálu, která tento nedostatek překonává, je McShaneův integrál , který lze nejsnáze definovat pomocí zobecněných Riemannových součtů.

Birkhoff integrál je také běžné zobecnění Bochnerův a Riemannův integrál. Na rozdíl od McShaneova integrálu však definice Birkhoffova integrálu nevyžaduje topologickou strukturu v definiční oblasti funkcí. Pokud jsou však splněny požadavky na integraci McShane, každá integrovatelná funkce Birkhoff může být také integrovatelná do McShane.

Kromě toho je Pettis integrál Za zmínku stojí další generalizace kroku. Používá funkčně-analytickou definici, ve které je integrovatelnost redukována na jednorozměrný případ: Nechť je to měřicí prostor . Funkce se nazývá Pettis-integrovatelná, pokud funkce Lebesgue-integrovatelná pro každou spojitou funkci a vektor existuje pro každou měřitelnou množinu , takže ${\ Displaystyle (\ Omega, {\ mathcal {A}}, \ mu)}$${\ Displaystyle f \ colon \ Omega \ to V}$${\ displaystyle \ lambda \ v V '}$${\ Displaystyle \ lambda \ circ f \ colon \ Omega \ to \ mathbb {R}}$${\ displaystyle A \ in {\ mathcal {A}}}$${\ displaystyle x_ {A} \ v V}$

${\ Displaystyle \ forall \ lambda \ in V '\ colon \ \ lambda (x_ {A}) = \ int _ {A} {\ lambda \ circle f} \, \ mathrm {d} \ mu}$

je použitelný. Vektor je poté vhodně pojmenován pomocí . ${\ displaystyle x_ {A}}$${\ Displaystyle \ textstyle \ int _ {A} f \, \ mathrm {d} \ mu}$

U funkcí, které nabývají hodnot v oddělitelném Banachově prostoru , integrál Pettis souhlasí s integrály McShane a Bochner. Nejdůležitějším zvláštním případem všech těchto definic je případ funkcí v , které jsou jednoduše integrovány komponenta po komponentě ve všech těchto definicích. ${\ Displaystyle f \ colon [a, b] \ až V}$${\ displaystyle V}$${\ displaystyle \ mathbb {R} ^ {n}}$

Zobecnění

Termín integrál byl rozšířen mnoha způsoby, některé varianty jsou:

• Riemannův integrál
• Daniellův integrál
• Stieltjesův integrál
• Itō integrál a Stratonowitschův integrál , viz také Diskrétní stochastický integrál
• Integrální měrka nebo Henstock-Kurzweilův integrál , zejména:
  • Integrál McShane
  • Pepřový integrál
• Změřte integrál
  • Lebesgueův integrál
  • Bochnerův integrál
  • Birkhoffův integrál
  • Pettisův integrál
  • Vlasový integrál
• Volkenborn integrál

Teorie měření

Chlupatá míra

Haarova míra, po Alfrédu Haarovi , představuje zobecnění Lebesgueova měřítka pro lokálně kompaktní topologické skupiny, a tedy také indukuje integrál jako zobecnění Lebesgueova integrálu.

Integrace na rozdělovačích

Viz: Integrace diferenciálních forem

Nakonec lze integraci použít také k měření povrchů daných těles. To vede do oblasti diferenciální geometrie .

Viz také

• Algebraická integrace
• Stochastická integrace
• Tabulka derivací a antiderivativ
• Volkenborn integrál

literatura

• Školní knihy:
  • Integrální počet je ústředním předmětem vyšší sekundární úrovně, a proto se jím zabývají všechny učebnice matematiky.
• Učebnice pro studenty matematiky a příbuzných předmětů (fyzika, informatika):
  • Herbert Amann, Joachim Escher : Analýza I, II, III. Birkhäuser-Verlag Basel Boston Berlin, ISBN 3-7643-7755-0 , ISBN 3-7643-7105-6 , ISBN 3-7643-6613-3 .
  • Richard Courant : Přednášky o diferenciálním a integrálním počtu 1, 2. Springer, 1. vydání 1928, 4. vydání 1971.
  • Gregor Michailowitsch Fichtenholz : Diferenciální a integrální počet I - III. Nakladatelství Harri Deutsch, Frankfurt nad Mohanem, 1990–2004. ISBN 978-3-8171-1418-4 (kompletní sada).
  • Otto Forster : Analýza 1. Diferenciální a integrální počet proměnných. 7. vydání. Vieweg-Verlag, 2004. ISBN 3-528-67224-2 .
  • Otto Forster: Analýza. Svazek 3: Teorie měření a integrace, integrální věty v R ⁿ a aplikacích , 8. vylepšené vydání. Springer Spectrum, Wiesbaden, 2017, ISBN 978-3-658-16745-5 .
  • Konrad Königsberger : Analýza. 2 svazky, Springer, Berlín 2004.
  • Vladimir Ivanovič Smirnov : Kurz vyšší matematiky (části 1–5). Nakladatelství Harri Deutsch, Frankfurt nad Mohanem, 1995–2004. ISBN 978-3-8171-1419-1 (kompletní sada).
  • Steffen Timmann: Repetitorium der Analysis 1, 2. 1. vydání. Binomi Verlag, 1993.
• Učebnice pro studenty s vedlejším / základním předmětem matematiky (např. Studenty strojírenství nebo ekonomie):
  • Rainer Ansorge a Hans Joachim Oberle: Matematika pro inženýry. Svazek 1. 3. vydání. Wiley-VCH, 2000.
  • Lothar Papula : Matematika pro přírodní vědce a inženýry. Svazek 1. 13. vydání. Vieweg + Teubner Verlag. ISBN 978-3-8348-1749-5 .
• Historický:
  • Adolph Mayer: Příspěvky k teorii maxim a minim jednoduchých integrálů. Teubner, Lipsko 1866 ( digitalizovaná verze ).
  • Bernhard Riemann: O reprezentovatelnosti funkce trigonometrickou řadou. Göttingen 1867 ( plné znění ), s první definicí Riemannova integrálu (strana 12 a násl.).

webové odkazy

• Online kalkulačka pro výpočet integrálů (antiderivativ) s výpočetní metodou a vysvětlivkami (německy)
• mathe-online.at - Zdroje na téma integrace (sekundární úroveň 2 / FHS / Uni)
• Jasná vysvětlení
• Integrator - anglické místo pro výpočet integrálů
• Integrální kalkulačka - německý web pro výpočet určitých a neurčitých integrálů (antiderivativa)
• Část 1 třídílné série o více integrálech (podrobná + rozsáhlá)
• 50 příkladů funkcí kořenových funkcí
• Video: integrální, antiderivativní . Jörn Loviscach 2010, zpřístupněn Knihovnou technických informací (TIB), doi : 10,5446 / 9752 .
• Video: derivace, integrál, náhoda . Jörn Loviscach 2010, zpřístupněn Knihovnou technických informací (TIB), doi : 10,5446 / 9736 .
• Video: jednoznačný integrál 1 . Jörn Loviscach 2010, zpřístupněn Knihovnou technických informací (TIB), doi : 10,5446 / 9755 .
• Video: jednoznačný integrál 2 . Jörn Loviscach 2010, zpřístupněn Knihovnou technických informací (TIB), doi : 10,5446 / 9756 .

Individuální důkazy

1. ↑ D. Fremlin: McShaneův a Birkhoffův integrál funkcí s vektorovou hodnotou. ( Memento z 28. dubna 2015 v internetovém archivu ).