Diferenciální forma

Termín diferenciální forma (často také nazývaný střídavá diferenciální forma) sahá až k matematikovi Élie Josephu Cartanovi . Diferenciální tvary jsou základním konceptem diferenciální geometrie . Umožňují integraci nezávislou na souřadnicích na obecně orientovaných diferencovatelných varietách .

kontext

Buď ${\ displaystyle U}$

• otevřená podmnožina${\ displaystyle \ mathbb {R} ^ {n}}$
• nebo rozlišitelný podmanifold z${\ displaystyle \ mathbb {R} ^ {n}}$
• nebo diferencovatelné potrubí .

V každém z těchto případů existuje

• koncept diferencovatelné funkce v prostoru nekonečně diferencovatelných funkcí při přechodu na určené;${\ displaystyle U;}$${\ displaystyle U}$${\ displaystyle C ^ {\ infty} (U)}$
• koncept tečného prostoru an v bodě${\ displaystyle \ mathrm {T} _ {p} U}$${\ displaystyle U}$${\ displaystyle p \ v U;}$
• koncept směrových derivací pro tangenciální vektor a diferencovatelnou funkci${\ displaystyle {\ tfrac {\ částečné f} {\ částečné X}}}$${\ displaystyle X \ in \ mathrm {T} _ {p} U}$${\ displaystyle f;}$
• pojem diferencovatelné vektorové pole v prostoru vektorových polí je označen.${\ displaystyle U;}$${\ displaystyle U}$${\ displaystyle \ Gamma (\ mathrm {T} U)}$

Duální prostor tangenty prostoru se nazývá cotangent prostor . ${\ displaystyle \ mathrm {T} _ {p} U}$ ${\ displaystyle \ mathrm {T} _ {p} ^ {*} U}$

definice

Diferenciální forma

Rozdíl forma míry na${\ displaystyle k}$${\ displaystyle U}$ nebo krátké formy je hladký řez v té vnější síly z Kotangentialbündels z . V symbolickém zápisu tento prostředek , přičemž kotangent svazek , th vnější síla , a tím i množství hladkých částí označeny. ${\ displaystyle k}$ ${\ displaystyle \ omega}$${\ displaystyle k}$${\ displaystyle U}$${\ displaystyle \ omega \ in \ Gamma (\ Lambda ^ {k} (T ^ {*} U))}$${\ displaystyle T ^ {*} U}$${\ displaystyle U}$${\ displaystyle \ Lambda ^ {k} (T ^ {*} U)}$${\ displaystyle k}$${\ displaystyle T ^ {*} U}$${\ displaystyle \ Gamma (\ Lambda ^ {k} (T ^ {*} U))}$${\ displaystyle \ Lambda ^ {k} (T ^ {*} U)}$

To znamená, že střídavý multilineární forma na tečné prostoru je přiřazena každému bodu ; takovým způsobem, že pro hladká vektorová pole funguje funkce ${\ displaystyle p \ v U}$ ${\ displaystyle \ omega _ {p}}$${\ displaystyle T_ {p} U}$${\ displaystyle k}$${\ displaystyle X_ {1}, \ ldots, X_ {k}}$

${\ displaystyle p \ mapsto \ omega _ {p} ((X_ {1}) _ {p}, \ ldots, (X_ {k}) _ {p}) \ in \ mathbb {R}}$

je plynulý , to znamená, že je možné jej libovolně odlišit.

Alternativně lze a -formu zobrazit jako alternativní plynulé multilineární mapování . To znamená: přiřadí funkci vektorovým polím tak, že ${\ displaystyle k}$${\ displaystyle \ omega}$${\ displaystyle \ omega \ colon (\ Gamma TU) ^ {k} \ do C ^ {\ infty} (U)}$${\ displaystyle \ omega}$${\ displaystyle k}$ ${\ displaystyle X_ {1}, \ ldots, X_ {k}}$${\ displaystyle \ omega (X_ {1}, \ ldots, X_ {k})}$

• ${\ displaystyle \ omega (X_ {1}, \ ldots, X '_ {i} + X' '_ {i}, \ ldots, X_ {k}) = \ omega (X_ {1}, \ ldots, X '_ {i}, \ ldots, X_ {k}) + \ omega (X_ {1}, \ ldots, X' '_ {i}, \ ldots, X_ {k})}$
• ${\ displaystyle \ omega (X_ {1}, \ ldots, f \ cdot X_ {i}, \ ldots, X_ {k}) = f \ cdot \ omega (X_ {1}, \ ldots, X_ {i}, \ ldots, X_ {k})}$ Pro ${\ displaystyle f \ v C ^ {\ infty} (U), 1 \ leq i \ leq k}$

a

• ${\ displaystyle \ omega (X_ {1}, \ ldots, X_ {i}, \ ldots, X_ {j}, \ ldots, X_ {k}) = - \ omega (X_ {1}, \ ldots, X_ { j}, \ ldots, X_ {i}, \ ldots, X_ {k})}$

platí.

Alternativa s využitím tenzorových polí : Forma je střídavé, kovariantní tenzorové pole úrovně${\ displaystyle k}$${\ displaystyle k.}$

Prostor diferenciálních forem

Sada formulářů tvoří vektorový prostor a je označena. Pokračujete v sázení ${\ displaystyle k}$${\ displaystyle U}$${\ displaystyle \ Omega ^ {k} (U)}$

${\ displaystyle \ Omega (U) = \ bigoplus _ {k = 1} ^ {\ infty} \ Omega ^ {k} (U).}$

U konečných-rozměrné variety tato částka je konečná, protože vektorový prostor je nulový vektorový prostor . Sada je algebra s vnějším součinem jako násobení a tedy opět vektorový prostor. Z topologického hlediska je tento prostor také svazkem . ${\ displaystyle k> \ dim U}$${\ displaystyle \ Omega ^ {k} (U)}$${\ displaystyle \ Omega (U)}$

Lze to chápat jako prvek vnější síly ; tedy vnější produkt (tj. produkt ve vnější algebře ) definuje mapy ${\ displaystyle \ omega _ {p}}$ ${\ displaystyle \ Lambda ^ {k} (T_ {p} ^ {*} U)}$${\ displaystyle \ klín}$

${\ displaystyle \ Omega ^ {k} (U) \ krát \ Omega ^ {\ ell} (U) \ až \ Omega ^ {k + \ ell} (U), \ quad (\ omega, \ eta) \ mapsto \ omega \ klín \ eta,}$

být skrz ${\ displaystyle \ omega \ klín \ eta}$

${\ displaystyle (\ omega \ klín \ eta) _ {p} = \ omega _ {p} \ klín \ eta _ {p}}$

je definován bod po bodu.

Tento produkt je odstupňovaný komutativní , platí

${\ displaystyle \ omega \ klín \ eta = (- 1) ^ {\ deg \ omega \ cdot \ deg \ eta} \ cdot \ eta \ klín \ omega;}$

kde označuje stupeň d. to znamená, pokud -forma je, pak je . Produkt dvou lichých forem je tedy ve všech ostatních kombinacích komutativní a komutativní. ${\ displaystyle \ deg \ omega}$${\ displaystyle \ omega,}$${\ displaystyle \ omega}$${\ displaystyle k}$${\ displaystyle \ deg \ omega = k}$

Příklady

• Hladké funkce jsou 0-formy.
• Formuláře Pfaff jsou 1-formuláře.

Znázornění souřadnic

Nechť je to -dimenzionální diferencovatelné potrubí. Pojďme se také předpokládat, z lokálního souřadného systému (mapa) . Pak ${\ displaystyle M}$${\ displaystyle n}$${\ displaystyle (U, x)}$

${\ displaystyle B = \ {\ mathrm {d} x_ {i_ {1}} | _ {p} \ klín \ ldots \ klín \ mathrm {d} x_ {i_ {k}} | _ {p} \ {\ velký |} \ i_ {1} <\ ldots <i_ {k} \}}$

základem , kde je celková diferenciál na tý souřadnic funkci . To znamená, že lineární forma je, na které se mapuje -tý základní vektor základny na 1 a všechny ostatní na 0. ${\ displaystyle \ Lambda ^ {k} (T_ {p} ^ {*} M).}$${\ displaystyle \ mathrm {d} x_ {i}}$${\ displaystyle i}$${\ displaystyle x_ {i}}$${\ displaystyle \ mathrm {d} x_ {i} | _ {p}}$${\ displaystyle T_ {p} (M)}$${\ displaystyle i}$${\ displaystyle \ textstyle {\ frac {\ částečné} {\ částečné x_ {1}}} | _ {p}, \ ldots, {\ frac {\ částečné} {\ částečné x_ {n}}} | _ {p }}$

Každá diferenciální forma má na každé mapě jedinečné zastoupení ${\ displaystyle \ omega \ in \ Omega ^ {k} (M)}$${\ displaystyle (U, x)}$

${\ displaystyle \ omega | _ {U} = \ součet _ {1 \ leq i_ {1} <\ ldots <i_ {k} \ leq n} a_ {i_ {1}, \ ldots, i_ {k}} \ , \ mathrm {d} x_ {i_ {1}} \ klín \ ldots \ klín \ mathrm {d} x_ {i_ {k}}}$

s vhodnými rozlišitelnými funkcemi ${\ displaystyle a_ {i_ {1}, \ ldots, i_ {k}}.}$

Znázornění souřadnic ukazuje, že jediný diferenciální tvar je pro nulový tvar . ${\ displaystyle k> n}$${\ displaystyle \ omega = 0}$

Externí derivát

Vnější derivací je operátor, který přiřadí diferenciální formu diferenciální formě. Pokud to vezmeme v úvahu na množině diferenciálních forem, tj. Na množině hladkých funkcí, odpovídá vnější derivace obvyklé derivaci funkcí. ${\ displaystyle k}$${\ displaystyle (k + 1)}$${\ displaystyle 0}$

definice

Vnější derivát a -formy se stává indukční pomocí Lie derivát a Cartanova vzorec${\ displaystyle \ mathrm {d} \ omega}$${\ displaystyle k}$${\ displaystyle \ omega}$

${\ displaystyle {\ mathcal {L}} _ {X} = i_ {X} \ circ \ mathrm {d} + \ mathrm {d} \ circ i_ {X}}$

Jsou definovány; existuje vektorové pole, Lieův derivát a substituce${\ displaystyle X}$${\ displaystyle {\ mathcal {L}} _ {X}}$${\ displaystyle i_ {X}}$${\ displaystyle X.}$

Například pokud je 1-forma, pak je ${\ displaystyle \ omega}$

${\ displaystyle ({\ mathcal {L}} _ {X} \ omega) (Y) = {\ mathcal {L}} _ {X} (\ omega (Y)) - \ omega ({\ mathcal {L} } _ {X} (Y)) = X \ omega (Y) - \ omega ([X, Y])}$

a

${\ displaystyle ((\ mathrm {d} \ circ i_ {X}) \ omega) (Y) = (\ mathrm {d} (\ omega (X))) (Y) = Y \ omega (X),}$

tak

${\ displaystyle \ mathrm {d} \ omega (X, Y) = X \ omega (Y) -Y \ omega (X) - \ omega ([X, Y])}$

pro vektorová pole ; Lež držák označuje . ${\ displaystyle X, Y}$${\ displaystyle [X, Y]}$

Obecný vzorec je

${\ displaystyle {\ begin {array} {rcl} \ mathrm {d} \ omega (X_ {0}, \ ldots, X_ {k}) & = & \ sum _ {i = 0} ^ {k} (- 1) ^ {i} X_ {i} \ omega (X_ {0}, \ ldots, {\ hat {X}} _ {i}, \ ldots, X_ {k}) + \\ [0,5em] && + \ sum _ {0 \ leq i <j \ leq k} (- 1) ^ {i + j} \ omega ([X_ {i}, X_ {j}], X_ {0}, \ ldots, {\ hat {X}} _ {i}, \ ldots, {\ hat {X}} _ {j}, \ ldots, X_ {k}) \ ,; \ end {pole}}}$

střecha v symbolu znamená , že je třeba vynechat odpovídající argument. ${\ displaystyle {\ hat {}}}$${\ displaystyle {\ hat {X}} _ {i}}$

vlastnosti

Vnější derivát má následující vlastnosti:

• Externí derivát je anti-derivát . To znamená, že je -lineární a platí pro Leibnizovo pravidlo${\ displaystyle \ mathrm {d}}$${\ displaystyle \ mathbb {R}}$${\ displaystyle \ alpha \ in \ Omega ^ {k} (U), \ beta \ in \ Omega ^ {l} (U)}$

${\ displaystyle \ mathrm {d} (\ alpha \ wedge \ beta) = \ mathrm {d} \ alpha \ wedge \ beta + (- 1) ^ {k} \ alpha \ wedge \ mathrm {d} \ beta.}$

• Nechte tedy vnější derivaci souhlasit s celkovým rozdílem .${\ displaystyle f \ v C ^ {\ infty} (U),}$
• ${\ displaystyle \ mathrm {d} ^ {2} = \ mathrm {d} \ circ \ mathrm {d} = 0}$
• Vnější derivát respektuje omezení. Nechte to být otevřené a pak platí následující : Vnější derivace se proto také nazývá lokální operátor.${\ displaystyle U \ podmnožina V \ podmnožina M}$${\ displaystyle \ alpha \ in \ Omega ^ {k} (V).}$${\ displaystyle \ mathrm {d} (\ alpha | _ {U}) = (\ mathrm {d} \ alpha) | _ {U}.}$

Tyto čtyři vlastnosti plně charakterizují externí derivaci. To znamená, že z těchto vlastností lze odvodit výše uvedený empirický vzorec. Pokud počítáte s vnější derivací, dáváte přednost výpočtu s vlastnostmi derivace a vyhněte se výše uvedenému vzorci.

Souřadnicová reprezentace vnější derivace

Vnější derivace diferenciální formy

${\ displaystyle \ omega = \ součet _ {1 \ leq i_ {1} <\ ldots <i_ {k} \ leq n} a_ {i_ {1}, \ ldots, i_ {k}} (x) \ cdot \ mathrm {d} x_ {i_ {1}} \ klín \ ldots \ klín \ mathrm {d} x_ {i_ {k}}}$

v souřadnicovém zastoupení je

${\ displaystyle \ mathrm {d} \ omega = \ součet _ {1 \ leq i_ {1} <\ ldots <i_ {k} \ leq n} \ mathrm {d} a_ {i_ {1}, \ ldots, i_ {k}} \ wedge \ mathrm {d} x_ {i_ {1}} \ wedge \ ldots \ wedge \ mathrm {d} x_ {i_ {k}}}$

s celkovými diferenciály funkcí koeficientu

${\ displaystyle \ mathrm {d} a_ {i_ {1}, \ ldots, i_ {k}} = \ součet _ {j = 1} ^ {n} {\ frac {\ částečné a_ {i_ {1}, \ ldots, i_ {k}}} {\ částečné x_ {j}}} \ mathrm {d} x_ {j}}$.

Chcete-li znovu vyjádřit výsledné výrazy prostřednictvím standardního základu, jsou to identity

${\ displaystyle \ mathrm {d} x_ {i} \ klín \ mathrm {d} x_ {j} = - \ mathrm {d} x_ {j} \ klín \ mathrm {d} x_ {i}}$

a

${\ displaystyle \ mathrm {d} x_ {i} \ klín \ mathrm {d} x_ {i} = 0}$

Důležité.

příklad

za pravdivý ${\ displaystyle n = 2, k = 1}$

${\ displaystyle {\ začátek {zarovnáno} \ mathrm {d} (a_ {1} \ cdot \ mathrm {d} x_ {1} + a_ {2} \ cdot \ mathrm {d} x_ {2}) & = \ mathrm {d} a_ {1} \ wedge \ mathrm {d} x_ {1} + \ mathrm {d} a_ {2} \ wedge \ mathrm {d} x_ {2} \\ [0.5em] & = \ left ({\ frac {\ částečné a_ {1}} {\ částečné x_ {1}}} \ mathrm {d} x_ {1} + {\ frac {\ částečné a_ {1}} {\ částečné x_ {2}} } \ mathrm {d} x_ {2} \ vpravo) \ klín \ mathrm {d} x_ {1} + \ vlevo ({\ frac {\ částečné a_ {2}} {\ částečné x_ {1}}} \ mathrm {d} x_ {1} + {\ frac {\ částečné a_ {2}} {\ částečné x_ {2}}} \ mathrm {d} x_ {2} \ vpravo) \ klín \ mathrm {d} x_ {2 } \\ [0.5em] & = {\ frac {\ částečné a_ {1}} {\ částečné x_ {1}}} \ cdot \ mathrm {d} x_ {1} \ klín \ mathrm {d} x_ {1 } + {\ frac {\ částečný a_ {1}} {\ částečný x_ {2}}} \ cdot \ mathrm {d} x_ {2} \ klín \ mathrm {d} x_ {1} + {\ frac {\ částečný a_ {2}} {\ částečný x_ {1}}} \ cdot \ mathrm {d} x_ {1} \ klín \ mathrm {d} x_ {2} + {\ frac {\ částečný a_ {2}} { \ částečné x_ {2}}} \ cdot \ mathrm {d} x_ {2} \ klín \ mathrm {d} x_ {2} \\ [0,5 em] & = \ left ({\ frac {\ částečné a_ {2 }} {\ částečné x_ {1}}} - {\ frac {\ částečné a_ {1}} {\ částečné x_ {2}}} \ pravé) \ cdot \ mathrm {d} x_ {1} \ klín \ mathrm {d} x_ {2}. \ end {zarovnáno}}}$

Obecně platí vnější derivace 1-formy

${\ displaystyle \ mathrm {d} \ left (\ sum _ {i = 1} ^ {n} a_ {i} \ cdot \ mathrm {d} x_ {i} \ right) = \ sum _ {1 \ leq i <j \ leq n} \ left ({\ frac {\ částečné a_ {j}} {\ částečné x_ {i}}} - {\ frac {\ částečné a_ {i}} {\ částečné x_ {j}}} \ right) \ cdot \ mathrm {d} x_ {i} \ klín \ mathrm {d} x_ {j}}$

Pro koeficienty vnější derivace 1-formy tvoří rotaci vektoru vytvořeného z koeficientů 1-formy. ${\ displaystyle n = 3}$

Další operace na diferenciálních formách

Vnitřní produkt

Nechť je hladké vektorové pole. Vnitřní produkt je lineární mapa ${\ displaystyle X \ v T (M)}$

${\ displaystyle i_ {X} \ dvojtečka \ Omega ^ {k} (M) \ až \ Omega ^ {k-1} (M),}$

podle

${\ displaystyle \ omega \ mapsto \ omega (X, \ cdot, \ ldots, \ cdot)}$

daný je. To znamená, že vnitřní produkt mapuje tvar na tvar vyhodnocením tvaru na pevném vektorovém poli . Toto mapování je analogem zúžení tenzoru v prostoru diferenciálních forem. Proto se této operaci někdy v angličtině říká „kontrakce“. ${\ displaystyle k}$${\ displaystyle \ omega}$${\ displaystyle (k-1)}$${\ displaystyle X}$

Vnitřní produkt je anti-derivace . To znamená, že pro a pravidlo Leibniz aplikuje${\ displaystyle i_ {X}}$${\ displaystyle \ omega \ in \ Omega ^ {k} (M)}$${\ displaystyle \ nu \ in \ Omega ^ {l} (M)}$

${\ displaystyle i_ {X} (\ omega \ klín \ nu) = (i_ {X} \ omega) \ klín \ nu + (- 1) ^ {k} \ omega \ klín (i_ {X} \ nu). }$

Platí také pro vnitřní produkt ${\ displaystyle i_ {X} \ circ i_ {X} = 0.}$

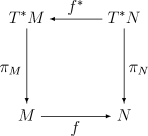
Zpětný transport (pullback) diferenciálních forem

Pokud je hladký mapování mezi diferencovatelné potrubí , pak v podobě získaných s je definována následujícím způsobem: ${\ displaystyle f \ dvojtečka M \ až N}$${\ displaystyle \ omega \ in \ Omega ^ {k} (N)}$${\ displaystyle f}$ ${\ displaystyle (f ^ {*} \ omega) \ v \ Omega ^ {k} (M)}$

${\ displaystyle (f ^ {*} \ omega) (X_ {1}, \ ldots, X_ {k}): = \ omega (\ mathrm {d} f (X_ {1}), \ ldots, \ mathrm { d} f (X_ {k}))}$

Je to způsobeno indukovanou mapou derivátů , která se nazývá „push-forward“. Odstoupení je kompatibilní s externím odtokem a externím produktem: ${\ displaystyle df \ colon TM \ to TN}$${\ displaystyle f}$

• ${\ displaystyle f ^ {*} (\ mathrm {d} \ omega) = \ mathrm {d} (f ^ {*} \ omega)}$

(napsáno podrobněji: na levé straně , proti ní na pravé straně ) a${\ displaystyle \ mathrm {d} = \ mathrm {d} ^ {(N)}}$${\ displaystyle \ mathrm {d} = \ mathrm {d} ^ {(M)}}$

• ${\ displaystyle f ^ {*} (\ omega \ klín \ eta) = (f ^ {*} \ omega) \ klín (f ^ {*} \ eta)}$

pro všechny ${\ displaystyle \ omega, \ eta \ in \ Omega ^ {pback} (N)}$

Zejména mapování mezi kohomologickými skupinami De Rham (viz níže) ${\ displaystyle f}$

${\ displaystyle f ^ {pback} \ colon \ mathrm {H} _ {\ mathrm {dR}} ^ {k} (N) \ longrightarrow \ mathrm {H} _ {\ mathrm {dR}} ^ {k} ( M),}$

Věnujte pozornost obrácení směru šipky opačně („pull-back“, „cohomology“ místo „homology“). ${\ displaystyle f \ dvojtečka M \ až N}$

Duální forma a hvězdný operátor

Vnější formy jsou uvažovány v -rozměrném prostoru, ve kterém je definován vnitřní produkt (metrický), takže lze vytvořit ortonormální základ prostoru. Forma dvojí vůči vnější formě stupně v tomto -rozměrném prostoru je -forma ${\ displaystyle n}$${\ displaystyle e_ {i}}$${\ displaystyle k}$${\ displaystyle n}$${\ displaystyle (nk)}$

${\ displaystyle * (e_ {1} \ klín e_ {2} \ klín \ ldots \ klín e_ {k}) = e_ {k + 1} \ klín e_ {k + 2} \ klín \ ldots \ klín e_ {n }.}$

Obě strany jsou psány v orientované formě. Duální forma je formálně označena pomocí operátora (Hodge) . Zejména pro diferenciální formy v trojrozměrném euklidovském prostoru byly získány následující výsledky: ${\ displaystyle *}$

${\ displaystyle * \ mathrm {d} x = \ mathrm {d} y \ klín \ mathrm {d} z}$

${\ displaystyle * \ mathrm {d} y = \ mathrm {d} z \ klín \ mathrm {d} x}$

${\ displaystyle * \ mathrm {d} z = \ mathrm {d} x \ klín \ mathrm {d} y}$

s 1 formuláři . Bylo vzato v úvahu, že orientovaný řád je zde a (cyklické přestupy v ). ${\ displaystyle dx, dy, dz}$${\ displaystyle (y, z), (z, x)}$${\ displaystyle (x, y)}$${\ displaystyle (x, y, z)}$

Symbol má zdůraznit skutečnost, že existuje vnitřní produkt v prostoru forem na podkladové prostoru , protože je možné napsat na dvě formy a jako objemový formu a integrálu ${\ displaystyle *}$${\ displaystyle M}$${\ displaystyle \ alpha \ klín * \ beta}$${\ displaystyle k}$${\ displaystyle \ alpha}$${\ displaystyle \ beta}$

${\ displaystyle (\ alpha, \ beta) = \ int _ {M} \ alpha \ klín * \ beta}$

vrací skutečné číslo. Sčítání dual znamená, že dvojitá aplikace na -form má za následek opět -form - kromě znaménka , které musí být zváženo samostatně. Přesněji, následující platí pro a -form v -dimenzionálním prostoru, jehož metrika má podpis ( v euklidovském prostoru, v Minkowského prostoru): ${\ displaystyle k}$${\ displaystyle k}$${\ displaystyle k}$${\ displaystyle n}$${\ displaystyle s}$${\ displaystyle s = + 1}$${\ displaystyle s = -1}$

${\ displaystyle ** \ alpha = (- 1) ^ {k (nk)} s \; \ alpha}$

Nahoře bylo ukázáno, jak v 3-dimenzionálním euklidovském prostoru 2-forma vede k externí derivaci 1-formy se složkami vektoru rotace vektorové analýzy jako koeficientů. Tito dva tvořit můžete použít -operator nyní formálně přímo jako jedna z forem ( red vektor) napiš: . Podobně se operátor používá k „překladu“ výše uvedené Stokesovy věty do formy vektorové analýzy. ${\ displaystyle \ alpha}$${\ displaystyle d \ klín \ alfa}$${\ displaystyle *}$${\ displaystyle * (d \ klín \ alfa)}$${\ displaystyle *}$

De Rhamova kohomologie

Z odstupňované algebry lze společně s vnější derivací sestrojit koketový komplex . Pro toto je pak porovnáno s obvyklými metodami homologické algebry jedna definovaná kohomologie . Georges de Rham dokázal, že tato po něm pojmenovaná kohomologická teorie souhlasí se singulární kohomologií . Chcete-li definovat De Rhamovu kohomologii, jsou nejprve definovány pojmy přesné a uzavřené diferenciální formy: ${\ displaystyle \ Omega (U)}$

Přesné a uzavřené formy

A -form se nazývá closed, pokud drží; nazývá se to přesné, pokud existuje -forma , která drží. Kvůli vzorci je každý přesný tvar uzavřen. Všimněte si, že blízkost, na rozdíl od přesnosti, je místní vlastnost: Je-li open cover of pak -forma je uzavřen pouze v případě omezení na je uzavřen pro každého . ${\ displaystyle k}$${\ displaystyle \ omega}$${\ displaystyle \ mathrm {d} \ omega = 0}$${\ displaystyle (k-1)}$${\ displaystyle \ eta}$${\ displaystyle \ omega = \ mathrm {d} \ eta}$${\ displaystyle \ mathrm {d} \ mathrm {d} \ eta = 0}$${\ displaystyle \ {V _ {\ alpha} \}}$${\ displaystyle U,}$${\ displaystyle k}$${\ displaystyle \ omega}$${\ displaystyle \ omega}$${\ displaystyle V _ {\ alpha}}$${\ displaystyle \ alpha}$

Kohomologické skupiny De Rham

Prostor faktoru

(Sada všech uzavřených formulářů zapnuta ) (sada všech přesných formulářů zapnuta )${\ displaystyle k}$${\ displaystyle U}$${\ displaystyle {\ big /}}$${\ displaystyle k}$${\ displaystyle U}$

se nazývá -th De Rhamova kohomologická skupina. Obsahuje informace o globální topologické struktuře${\ displaystyle k}$ ${\ displaystyle \ mathrm {H} _ {\ mathrm {dR}} ^ {k} (U).}$${\ displaystyle U.}$

Poincarého lemma

Poincaréovo lemma říká, že pro a hvězdné oblasti . Obecněji řečeno, prohlášení tohoto lemmatu se vztahuje na smrštitelných otevřených podmnožin v Důkazem je konstruktivní, i. To znamená, že jsou konstruovány explicitní příklady, což je pro aplikace velmi důležité. Všimněte si, že se skládá z lokálně konstantních funkcí , protože podle definice neexistují žádné přesné formy 0. Takže je pro každého${\ displaystyle \ mathrm {H} _ {\ mathrm {dR}} ^ {k} (U) = 0}$${\ displaystyle k> 0}$ ${\ displaystyle U}$${\ displaystyle U}$${\ displaystyle \ mathbb {R} ^ {n}.}$${\ displaystyle \ mathrm {H} _ {\ mathrm {dR}} ^ {0} (U)}$${\ displaystyle \ mathrm {H} _ {\ mathrm {dR}} ^ {0} (U) \ not = 0}$${\ displaystyle U \ neq \ varnothing.}$

Pokud je uzavřený a přesný, následuje ${\ displaystyle \ omega}$${\ displaystyle \ eta = \ mathrm {d} \ eta '}$

${\ displaystyle \ omega \ klín \ eta = \ omega \ klín \ mathrm {d} \ eta '= (- 1) ^ {\ deg \ omega} \ mathrm {d} (\ omega \ klín \ eta') \, .}$

Totéž platí, pokud je přesné a uzavřené. Existují tedy indukovaná zobrazení ${\ displaystyle \ omega}$${\ displaystyle \ eta}$

${\ displaystyle \ mathrm {H} _ {\ mathrm {dR}} ^ {k} (U) \ krát H _ {\ mathrm {dR}} ^ {m} (U) \ longrightarrow \ mathrm {H} _ { \ mathrm {dR}} ^ {k + m} (U).}$

Příklad z elektrodynamiky

V elektrodynamiky, což znamená, lemma Poincaré , že pro každou dvojici elektromagnetických polí, na dvoustupňovém střídavý diferenciálním tvaru v čtyřrozměrného Minkowski prostoru lze shrnout, jednostupňové vektorový potenciál forma s existuje takzvaný „čtyři -potenciál ", viz také čtyři vektory . Hustotu proudu a náboje lze také kombinovat a vytvořit čtyřvektorový nebo odpovídající 3formový . ${\ displaystyle {\ vec {E}}, {\ vec {B}}}$${\ displaystyle \ mathbf {F}}$${\ displaystyle \ mathbf {A}}$${\ displaystyle \ mathbf {F} = \ mathrm {d} \ mathbf {A}}$${\ displaystyle \ mathbf {j}}$

Relativistické Maxwellovy rovnice elektrodynamiky na čtyřrozměrném časoprostorovém potrubí (s metrikou a determinantem metriky , přičemž zde samozřejmě existuje podpis Minkowského prostoru , například pro podle definice prvku čáry ) jsou například pomocí této symboliky: ${\ displaystyle M}$${\ displaystyle g _ {\ alpha, \ beta}}$${\ displaystyle g}$${\ displaystyle \ mathrm {diag} (+ 1, -1, -1, -1)}$${\ displaystyle \ alpha = 0,1,2,3,}$ ${\ displaystyle \ mathrm {ds}}$

${\ displaystyle \ mathrm {d} \ mathbf {F} = 2 (\ částečné _ {\ gamma} F _ {\ alpha \ beta} + \ částečné _ {\ beta} F _ {\ gamma \ alfa} + \ částečné _ {\ alpha} F _ {\ beta \ gamma}) \ mathrm {d} \, x ^ {\ alpha} \ klín \ mathrm {d} \, x ^ {\ beta} \ klín \ mathrm {d} \ , x ^ {\ gamma} = 0}$

(tzv. Bianchi identita ) a

${\ displaystyle \ mathrm {d} (* \ mathbf {F}) = {F ^ {\ alpha \ beta}} _ {; \ alpha} {\ sqrt {-g}} \, \ epsilon _ {\ beta \ gamma \ delta \ eta} \ mathrm {d} \, x ^ {\ gamma} \ klín \ mathrm {d} \, x ^ {\ delta} \ klín \ mathrm {d} \, x ^ {\ eta} = \ mathbf {j}}$

s tenzorem elektromagnetického pole vyjádřeným jako 2-forma

${\ displaystyle \ mathbf {F} = F _ {\ alpha \ beta} \, \ mathrm {d} \, x ^ {\ alpha} \ klín \ mathrm {d} \, x ^ {\ beta} \ ,, }$

z. B. se složkou vektoru magnetické indukce a s proudem (zapsáno jako 3-forma) ${\ displaystyle F_ {1,2} = B_ {z}}$${\ displaystyle z}$

${\ displaystyle \ mathbf {j} = j ^ {\ alpha} {\ sqrt {-g}} \, \ epsilon _ {\ alpha \ beta \ gamma \ delta} \ mathrm {d} \, x ^ {\ beta } \ wedge \ mathrm {d} \, x ^ {\ gamma} \ wedge \ mathrm {d} \, x ^ {\ delta}.}$

Zde je symbol anti-symetrizace ( symbol Levi-Civita ) a středník znamená kovariantní derivaci . Jako obvykle se přidají dvojitě se vyskytující indexy ( Einsteinova součtová konvence ) a použijí se přirozené jednotky (rychlost světla nahrazena ). Použitím operátoru lze alternativně zapsat druhou sadu čtyř Maxwellových rovnic s 1 formou pro aktuální. Z Maxwellových rovnic je to vidět a dodržovat velmi odlišné rovnice v elektrodynamice, takže dualita není symetrií této teorie. Je to proto, že dualita si vyměňuje elektrická a magnetická pole, ale v elektrodynamice nejsou známy žádné magnetické monopoly. Volné Maxwellovy rovnice, jejichž výsledkem je , na druhé straně, mají dvojí symetrii. ${\ displaystyle \ epsilon _ {\ alfa \ beta \ gama \ delta}}$${\ displaystyle c}$${\ displaystyle 1}$${\ displaystyle *}$${\ displaystyle \ mathbf {F}}$${\ displaystyle * \ mathbf {F}}$${\ displaystyle \ mathbf {j} \ equiv 0}$

Potenciál forma je pouze jednoznačné výjimkou jedné přísady kromě : a vedou ke stejné s kalibračním formě , která je splněna, ale jinak libovolné. Tuto další takzvanou volnost kalibrace lze použít ke splnění dalších omezení v určitých bodech. Například v elektrodynamice se vyžaduje, aby všude platila další takzvaná Lorenzova podmínka ( Lorenzova kalibrace ) ; tato podmínka je ve čtyřech složkách jednoduchá . Tato „kalibrační fixace“ nakonec vede k takzvanému „retardovanému potenciálu“ jako jedinečnému řešení všech čtyř Maxwellových rovnic: ${\ displaystyle \ mathbf {A}}$${\ displaystyle \ mathrm {d} \ chi}$${\ displaystyle \ mathbf {A}}$${\ displaystyle \ mathbf {A} + \ mathrm {d} \ chi}$${\ displaystyle \ mathbf {F},}$ ${\ displaystyle \ chi}$${\ displaystyle \ mathrm {d} (\ mathrm {d} \ chi) \ equiv 0}$${\ displaystyle \ mathbf {A}}$${\ displaystyle \ mathrm {d} (* \ mathbf {A}) = 0}$${\ displaystyle \ částečné _ {\ nu} A ^ {\ nu} = 0}$

${\ displaystyle A ^ {\ nu} (\ mathbf {r}, t) = \ int \, {\ frac {j ^ {\ nu} (\ mathbf {r '}, t - {\ frac {| \ mathbf {r} - \ mathbf {r '} |} {c}})} {4 \ pi | \ mathbf {r} - \ mathbf {r'} |}} \, \ mathrm {d} ^ {3} r '}$

Při přechodu na duál je třeba poznamenat, že nemáte co do činění s tím, ale s tím, kdo nese jinou metriku, konkrétně metodu Minkowski . Lineární prvek neměnný v Lorentzových transformacích je tam, kde je diferenci správný čas a byla použita konvence součtu. Ko- a kontravariantní čtyři vektorové komponenty se nyní liší. Je to pravda, ale a${\ displaystyle \ mathbb {R} ^ {4},}$${\ displaystyle \ mathbb {M} ^ {4}}$${\ displaystyle \ mathrm {d} s ^ {2} = - c ^ {2} \ mathrm {d} \ tau ^ {2} = dx ^ {2} + dy ^ {2} + dz ^ {2} - c ^ {2} dt ^ {2} = - \ mathrm {d} x _ {\ nu} \ mathrm {d} x ^ {\ nu},}$${\ displaystyle \ mathrm {d} \ tau}$${\ displaystyle + \ mathrm {d} x_ {0} \ equiv + \ mathrm {d} x ^ {0} = c \, dt,}$${\ displaystyle - \ mathrm {d} x_ {1} \ equiv + \ mathrm {d} x ^ {1} = dx,}$ ${\ displaystyle - \ mathrm {d} x_ {2} \ equiv + \ mathrm {d} x ^ {2} = dy}$${\ displaystyle - \ mathrm {d} x_ {3} \ equiv + \ mathrm {d} x ^ {3} = dz.}$

Teorie integrace

orientace

Pokud se jedná o název -formu, na kterém nezmizí žádný bod, nazývá se orientace na spolu s takovým tvarem orientovaný. Orientace definuje orientace tangenciálního a kotangensního prostoru: Základna kotangensového prostoru v bodě je pozitivně orientována, pokud ${\ displaystyle n = \ dim U,}$${\ displaystyle n}$${\ displaystyle U,}$${\ displaystyle U.}$ ${\ displaystyle U}$${\ displaystyle \ alpha}$${\ displaystyle \ eta _ {1}, \ ldots, \ eta _ {n}}$${\ displaystyle p}$

${\ displaystyle \ alpha _ {p} = a \ cdot \ eta _ {1} \ klín \ ldots \ klín \ eta _ {n}}$

s kladným číslem platí. Základna tečného prostoru v bodě je pozitivně orientována, pokud ${\ displaystyle a}$${\ displaystyle X_ {1}, \ ldots, X_ {n}}$${\ displaystyle p}$

${\ displaystyle \ alpha (X_ {1}, \ ldots, X_ {n})> 0}$

platí.

O dvou orientacích se říká, že jsou rovnocenné, pokud se liší pouze univerzálně pozitivním faktorem; tato podmínka je ekvivalentní definování stejné orientace na každém tangenciálním nebo kotangensním prostoru.

Pokud jsou připojeny , existují buď žádné, nebo přesně dvě třídy rovnocennosti. ${\ displaystyle U}$

${\ displaystyle U}$znamená orientovatelný, pokud existuje orientace . ${\ displaystyle U}$

Integrace diferenciálních forem

Nech to být znovu a předpokládáme, že byla zvolena orientace. Pak existuje kanonický integrál ${\ displaystyle n = \ dim U,}$${\ displaystyle U}$

${\ displaystyle \ int _ {U} \ omega}$

for -forms je otevřená podmnožina , standardní souřadnicové funkce jsou im a jsou ${\ displaystyle n}$${\ displaystyle \ omega.}$${\ displaystyle U}$${\ displaystyle \ mathbb {R} ^ {n}}$${\ displaystyle x_ {1}, \ ldots, x_ {n}}$${\ displaystyle \ mathbb {R} ^ {n}}$

${\ displaystyle \ omega = f \, \, \ mathrm {d} x_ {1} \ klín \ ldots \ klín \ mathrm {d} x_ {n},}$

tak:

${\ displaystyle \ int _ {U} \ omega = \ int _ {U} f (x_ {1}, \ tečky, x_ {n}) \, \, \ mathrm {d} x_ {1} \ ldots \ mathrm {d} x_ {n}}$

Integrál vpravo je obyčejný Lebesgueův integrál im${\ displaystyle \ mathbb {R} ^ {n}.}$

Pokud je -rozměrně orientované potrubí otevřené a mapa, pak se definuje ${\ displaystyle M}$${\ displaystyle n}$${\ displaystyle U \ podmnožina M}$${\ displaystyle \ phi \ dvojtečka U \ až \ mathbb {R} ^ {n}}$

${\ displaystyle \ int _ {U} \ omega = \ int _ {\ phi (U)} (\ phi ^ {- 1}) ^ {*} \ omega}$

jako integrál -formy nad mapovou oblastí . Diferenciální forma je přivedl zpět do otevřeného podmnožinu s parametrizace z a poté integrována podle výše uvedené definice. Z věty o transformaci vyplývá, že tato definice je invariantní ke koordinaci změn. ${\ displaystyle n}$${\ displaystyle \ omega}$${\ displaystyle U}$${\ displaystyle \ omega}$${\ displaystyle \ phi ^ {- 1} \ dvojtečka \ phi (U) \ do U}$${\ displaystyle U}$${\ displaystyle \ phi (U) \ podmnožina \ mathbb {R} ^ {n}}$

V případě, obecněji je měřitelná podmnožina , pak definuje ${\ displaystyle B}$${\ displaystyle U}$

${\ displaystyle \ int _ {B} \ omega = \ int _ {U} \ chi _ {B} \ omega}$

s charakteristickou funkcí , d. tj. je nastaven mimo nulu. ${\ displaystyle \ chi _ {B}}$${\ displaystyle \ omega}$${\ displaystyle B}$

K definování integrálu v celku lze použít rozklad ${\ displaystyle M}$

${\ displaystyle M = \ bigcup _ {j = 1} ^ {\ infty} M_ {j}}$

lze vybrat v spočetném počtu párových disjunktních měřitelných podmnožin , takže každá je zcela obsažena v jedné oblasti mapy . Takže vsadíte ${\ displaystyle M_ {j}}$${\ displaystyle M_ {j}}$${\ displaystyle U_ {j}}$

${\ displaystyle \ int _ {M} \ omega = \ součet _ {j = 1} ^ {\ infty} \ int _ {M_ {j}} \ omega}$.

Následující věta o transformaci platí pro integrály diferenciálních forem: Pokud existuje difeomorfismus zachovávající orientaci , pak platí pro${\ displaystyle f \ dvojtečka M \ až N}$${\ displaystyle \ omega \ in \ Omega ^ {n} (N)}$

${\ displaystyle \ int _ {N} \ omega = \ int _ {M} f ^ {*} \ omega}$

s načteným formulářem . ${\ displaystyle M}$${\ displaystyle f ^ {*} \ omega}$

Stokesova věta

Pokud je kompaktní, orientovaný -dimenzionální diferencovatelný potrubí s hranicí a opatřený indukovanou orientací, pak platí pro každý -form${\ displaystyle M}$${\ displaystyle n}$ ${\ displaystyle \ částečné M}$${\ displaystyle \ částečné M}$${\ displaystyle (n-1)}$${\ displaystyle \ omega}$

${\ displaystyle \ int _ {M} \ mathrm {d} \ omega = \ int _ {\ částečné M} \ omega.}$

Tato věta je dalekosáhlým zobecněním hlavní věty diferenciálního a integrálního počtu . Obsahuje Gaussovu integrální větu a klasickou integrální větu od Stokese jako speciální případy .

Pokud je uzavřeno , to znamená, že následuje pro každý přesný -form d. H. pro vztah ${\ displaystyle M}$ ${\ displaystyle \ částečné M = \ emptyset,}$ ${\ displaystyle n}$${\ displaystyle \ omega ^ {\ text {přesný}},}$${\ displaystyle \ omega \ equiv \ omega ^ {\ text {přesný}} = \ mathrm {d} \ varphi,}$

${\ displaystyle \ int _ {M} \ omega ^ {\ text {přesný}} = \ int _ {M} \ mathrm {d} \ varphi = \ int _ {\ částečný M = \ emptyset} \ varphi = 0. }$

K objasnění zmíněné vlastnosti se často používá formulace s kruhovým integrálem: ${\ displaystyle M}$

${\ displaystyle \ mast _ {M} \ omega ^ {\ text {přesný}} = 0}$

Integrál poskytuje mapu

${\ displaystyle \ mathrm {H} _ {\ mathrm {dR}} ^ {n} (M) \ do \ mathbb {R}.}$

Pokud je připojeno , toto mapování je izomorfismus . Tím se vrátíte zpět k cohomologii De Rham (viz výše). ${\ displaystyle M}$

Ukázkové výpočty

Na základě pravoúhlých souřadnic jsou 1-form ${\ displaystyle \ mathbb {R} ^ {3}}$ ${\ displaystyle (x, y, z)}$

${\ displaystyle \ omega = z ^ {2} \, \ mathrm {d} x + 2y \, \ mathrm {d} y + xz \, \ mathrm {d} z}$

a 2-forma

${\ displaystyle \ nu = z \, \ mathrm {d} z \ klín \ mathrm {d} x}$

daný.

Pro externí produkt platí následující:

${\ displaystyle \ omega \ klín \ nu = z ^ {3} \, \ podpona {\ mathrm {d} x \ klín \ mathrm {d} z \ klín \ mathrm {d} x} _ {= \, 0} + 2yz \, \ underbrace {\ mathrm {d} y \ wedge \ mathrm {d} z \ wedge \ mathrm {d} x} _ {= \, \ mathrm {d} x \ wedge \ mathrm {d} y \ klín \ mathrm {d} z} + xz ^ {2} \, \ podprsenka {\ mathrm {d} z \ klín \ mathrm {d} z \ klín \ mathrm {d} x} _ {= \, 0} = 2yz \, \ mathrm {d} x \ klín \ mathrm {d} y \ klín \ mathrm {d} z}$

Vnější derivace dává ${\ displaystyle \ omega}$

${\ displaystyle \ mathrm {d} \ omega = 2z \, \ mathrm {d} z \ klín \ mathrm {d} x + 2 \, \ mathrm {d} y \ klín \ mathrm {d} y + (z \ , \ mathrm {d} x + x \, \ mathrm {d} z) \ klín \ mathrm {d} z = 2z \, \ mathrm {d} z \ klín \ mathrm {d} xz \, \ mathrm {d } z \ klín \ mathrm {d} x = z \, \ mathrm {d} z \ klín \ mathrm {d} x}$,

ano . Zejména je přesný a následně uzavřený, tj. H. . To lze ověřit přímým výpočtem: . ${\ displaystyle \ mathrm {d} \ omega = \ nu}$${\ displaystyle \ nu}$${\ displaystyle \ mathrm {d} \ nu = 0}$${\ displaystyle \ mathrm {d} \ nu = \ mathrm {d} z \ klín \ mathrm {d} z \ klín \ mathrm {d} x = 0}$

Dále je dán , následované , , a , , pro on dohledat: ${\ displaystyle c \ colon [0,1] \ to \ mathbb {R} ^ {3}}$${\ displaystyle c (t) = (t ^ {2}, 2t, 1)}$${\ displaystyle x = t ^ {2}}$${\ displaystyle y = 2t}$${\ displaystyle z = 1}$${\ displaystyle \ mathrm {d} x = 2t \, \ mathrm {d} t}$${\ displaystyle \ mathrm {d} y = 2 \, \ mathrm {d} t}$${\ displaystyle \ mathrm {d} z = 0}$${\ displaystyle [0,1]}$

${\ displaystyle c ^ {*} \ omega = 2t \, \ mathrm {d} t + 8t \, \ mathrm {d} t = 10t \, \ mathrm {d} t}$

Pro integrál nad křivkou im dané takto výsledky ${\ displaystyle \ omega}$${\ displaystyle c}$${\ displaystyle \ Gamma = c ([0,1])}$${\ displaystyle \ mathbb {R} ^ {3}}$

${\ displaystyle \ int _ {\ Gamma} \ omega = \ int _ {[0,1]} c ^ {*} \ omega = \ int _ {0} ^ {1} 10 t \, \ mathrm {d} t = 5}$.

Pokud je jednotková koule uvnitř , pak je okraj jednotkové sféry tedy . Podle Stokesovy věty máme, protože${\ displaystyle S ^ {2} = \ {\ mathbf {x} \ in \ mathbb {R} ^ {3} \ {\ big |} \ \ | \ mathbf {x} \ | _ {2} = 1 \ }}$${\ displaystyle \ mathbb {R} ^ {3}}$${\ displaystyle S ^ {2}}$ ${\ displaystyle B ^ {3} = \ {\ mathbf {x} \ in \ mathbb {R} ^ {3} \ {\ big |} \ \ | \ mathbf {x} \ | _ {2} <1 \ }}$${\ displaystyle S ^ {2} = \ částečné B ^ {3}}$${\ displaystyle \ mathrm {d} \ nu = 0}$

${\ displaystyle \ int _ {S ^ {2}} \ nu = \ int _ {B ^ {3}} \ mathrm {d} \ nu = 0}$.

Například tvar 3 lze integrovat pomocí kostky jednotky . Jeho integrál souhlasí s Lebesgueovým integrálem koeficientové funkce : ${\ displaystyle \ omega \ klín \ nu}$${\ displaystyle W = [0,1] ^ {3}}$${\ displaystyle (x, y, z) \ mapsto 2yz}$

${\ displaystyle \ int _ {W} \ omega \ klín \ nu = \ int _ {W} 2yz \, \ mathrm {d} x \ klín \ mathrm {d} y \ klín \ mathrm {d} z = \ int _ {0} ^ {1} \ int _ {0} ^ {1} \ int _ {0} ^ {1} 2yz \, \ mathrm {d} x \, \ mathrm {d} y \, \ mathrm { d} z = 2 \ cdot \ int _ {0} ^ {1} y \, \ mathrm {d} y \ cdot \ int _ {0} ^ {1} z \, \ mathrm {d} z = {\ frac {1} {2}}}$.

Složité diferenciální formy

V teorii komplexních diferenciálních forem se zde zavedený počet přenáší do složitých variet . Z větší části to funguje analogicky k definici zde popsaných forem. Analogicky ke komplexním číslům se však prostory komplexních diferenciálních forem převádějí na dva prostory (skutečných) diferenciálních forem

${\ displaystyle {\ mathcal {E}} ^ {r} (M) \ cong \ Omega ^ {r, r} (M) = \ Omega ^ {r} (M) \ oplus i \ Omega ^ {r} ( M)}$

rozebrán. Prostor se pak nazývá prostor forem. Analogicky k vnější derivaci lze v těchto prostorech definovat dvě nové derivace. Jedná se o Dolbeault- volal a Dolbeault cross operátor, a podobně jako De Rham cohomology může být pomocí cross-Dolbeault operátor opět cohomology formě. Tomu se říká Dolbeaultova kohomologie . ${\ displaystyle \ Omega ^ {p, q}}$${\ displaystyle (p, q)}$

Viz také

Vektorové oceňované diferenciální formy

literatura

• Herbert Amann, Joachim Escher : Analýza III. 2. vydání. Birkhäuser, Basel 2008, ISBN 978-3-7643-8883-6 , kapitoly XI a XII.
• Henri Cartan : Diferenciální formy. Bibliographisches Institut, Mannheim 1974, ISBN 3-411-01443-1 .
• Klaus Jänich : Vektorová analýza. 5. vydání. Springer, Berlin / Heidelberg 2005, ISBN 978-3-540-27338-7 .
• Shigeyuki Morita: Geometrie diferenciálních forem. Americká matematická společnost 2001, ISBN 0821810456 .
• Harley Flanders : Diferenciální formy s aplikacemi na fyzikální vědy. Academic Press, 1963.
• Harold Edwards : Advanced Calculus - přístup diferenciálních forem. Birkhäuser, 1994 (první v roce 1969).
• Steven H. Weintraub : Diferenciální formy - doplněk vektorového počtu. Academic Press, 1997.

webové odkazy

• Gunnar Fløystad: Vnější algebra a centrální pojmy v matematice. (PDF; 182 kB). Oznámení AMS, svazek 62, 2015, č. 4.
• Diferenciální forma v nLab.