Metoda nejmenších čtverců

Metoda nejmenších čtverců (krátké MKQ nebo anglicky metodou nejmenších čtverců , nebo jen nejmenších čtverců krátkých: LS , na rozšíření vymezení z nich odvozených, jako je generalizovaná metodou nejmenších čtverců , nebo dvoustupňový způsob nejmenších čtverců také nazývá „obyčejné“ s dodatkem, že obyčejné nejmenší čtverce ( anglicky obyčejné nejmenší čtverce , zkráceně: OLS )) nebo metoda KQ (zastaralá metoda součtu nejmenších odchylek čtverců ) jsou standardní matematické postupy pro úpravu . V tomto případě, na A sadu datových bodů z funkce , určuje běží tak blízko, jak je to možné do datových bodů a tím nejlepší možné shrnující data. Nejčastěji používanou funkcí je přímka , které se pak říká přímka . Aby bylo možné tuto metodu použít, musí funkce obsahovat alespoň jeden parametr . Tyto parametry jsou pak metodou určeny tak, že když je funkce porovnána s datovými body a vzdálenost mezi hodnotou funkce a datovým bodem je čtvercová, součet těchto čtvercových vzdáleností je co nejmenší. Vzdálenosti se pak nazývají zbytky .

Tato metoda se obvykle používá ke zkoumání skutečných dat, jako jsou fyzické nebo ekonomické naměřené hodnoty . Tato data často obsahují nevyhnutelné chyby měření a kolísání . Za předpokladu, že se naměřené hodnoty blíží základním „ skutečným hodnotám “ a že mezi naměřenými hodnotami existuje určitý vztah, lze tuto metodu použít k nalezení funkce, která tento vztah dat co nejlépe popisuje . Metodu lze také použít obráceně k testování různých funkcí a tím k popisu neznámého vztahu v datech.

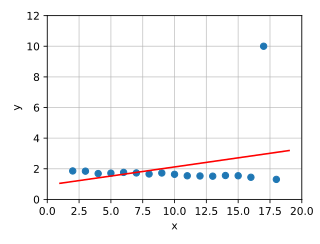
V ukázkové grafice jsou zadány datové body a kompenzační funkce. Je vybrána obecná funkce (funkce modelu ), která by měla odpovídat otázce a datům, v tomto případě logistické funkci . Jejich parametry jsou nyní určeny tak, aby byl minimalizován součet čtvercových odchylek pozorování od hodnot funkce . Na grafu je odchylka v tomto bodě viditelná jako svislá vzdálenost mezi pozorováním a křivkou. ${\ displaystyle e}$${\ displaystyle y}$${\ displaystyle e}$${\ displaystyle x}$${\ displaystyle y}$

Ve stochastice se metoda nejmenších čtverců většinou používá jako metoda odhadu regresní analýzy , kde se také označuje jako odhad nejmenších čtverců nebo obyčejný odhad nejmenších čtverců . Protože odhad nejmenších čtverců minimalizoval zbytkový součet , je to metoda odhadu, která obsahuje stanovení maximalizované. Metoda nejmenších čtverců se používá jako identifikace systému v souvislosti s modelovými experimenty, např. B. pro inženýry východisko z paradoxní situace určování parametrů modelu pro neznámé zákony.

příběh

Na Nový rok 1801 objevil italský astronom Giuseppe Piazzi trpasličí planetu Ceres . Byl schopen sledovat cestu 40 dní, poté Ceres zmizel za sluncem. V průběhu roku se mnoho vědců neúspěšně pokusilo vypočítat oběžnou dráhu na základě Piazziho pozorování - za předpokladu kruhové oběžné dráhy, protože v té době mohly být oběžné prvky pro ně pouze matematicky určeny z pozorovaných poloh oblohy.

24letému Gaussovi se podařilo vypočítat oběžnou dráhu pomocí nové nepřímé metody určování oběžné dráhy a jeho kompenzačních výpočtů založených na metodě nejmenších čtverců (i když ještě nebyla tak označena) takovým způsobem, že Franz Xaver von Zach ho našel 7. prosince 1801 a - potvrzeno - 31. prosince 1801. Heinrich Wilhelm Olbers to potvrdil nezávisle na Zachovi pozorováním 1. a 2. ledna 1802.

Problém při hledání Ceres jako takového byl ten, že pozorování nezpůsobila ani polohu, část oběžné dráhy, ani známou vzdálenost , ale pouze směry pozorování. To vede k hledání elipsy a ne kruhu, jak navrhují Gaussovi konkurenti. Je znám jeden z ohniskových bodů elipsy (samotné slunce ) a oblouky oběžné dráhy Ceres mezi směry pozorování procházejí podle druhého Keplerova zákona , to znamená, že časy se chovají jako povrchy smetené vodicí paprsek. Kromě toho je pro výpočetní řešení známo, že samotná pozorování jsou založena na kuželovitém úseku v prostoru, samotné oběžné dráze Země.

Problém v zásadě vede k rovnici osmého stupně, jejíž triviální řešení je samotná oběžná dráha Země. Díky rozsáhlým sekundárním podmínkám a (později) metodě nejmenších čtverců vyvinuté Gaussem se 24letému muži podařilo určit polohu, kterou vypočítal pro oběžnou dráhu Ceres od 25. listopadu do 31. prosince 1801. To Zachovi umožnilo najít Ceres v poslední den předpovědi. Místo nebylo menší než 7 ° (tj. 13,5  šířky úplňku ) na východ od místa, kde ostatní astronomové podezřívali Ceres, kterému nejen Zach, ale i Olbers řádně vzdali hold.

Jeho první výpočty byly stále bez metody nejmenších čtverců , pouze když bylo po znovuobjevení Cerese k dispozici mnoho nových dat, použil je k přesnějšímu určení orbitálních prvků, ale bez obecného odhalení podrobností své metody. Obnovila se také Piazziho pověst, která těžce utrpěla kvůli bodům cesty, které nechtěly vejít na kruhovou cestu.

Předchůdcem metody nejmenších čtverců je metoda nejmenších absolutních odchylek , kterou vyvinul v roce 1760 Rugjer Josip Bošković . Gauss vyvinul základy metody nejmenších čtverců již v roce 1795 ve věku 18 let. Vycházel z myšlenky Pierra-Simona Laplaceho sečíst odchylky naměřených hodnot od očekávané hodnoty takovým způsobem, že součet všech těchto takzvaných chyb vyústil v nulu. Na rozdíl od této metody Gauss místo chyb použil čtverce chyb a byl tak schopen upustit od požadavku nulového součtu. Nezávisle na Gaussovi vyvinul Francouz Adrien-Marie Legendre stejnou metodu, poprvé ji publikoval v roce 1805, na konci malé práce na výpočtu drah komet, a vydal druhé pojednání o ní v roce 1810. Její prezentace byla extrémně jasná a jednoduché. Název Méthode des moindres carrés (metoda nejmenších čtverců) také pochází z Legendre .

V roce 1809 publikoval Gauss ve druhém svazku svého nebeského mechanického díla Theoria motus corporum coelestium in sectionibus conicis solem ambientium (teorie pohybu nebeských těles, která se v kuželových řezech otáčejí kolem Slunce), metoda zahrnující normální rovnice, stejně jako Gaussova eliminační metoda a Gauss-Newtonova metoda , která šla daleko za Legendre. V něm označil za svůj objev metodu nejmenších čtverců a tvrdil, že ji objevil a použil již v roce 1795 (tj. Před Legendrem), což ho dlouho štvalo. Legendre si na to stěžoval v dlouhém dopise Gaussovi, který Gauss ponechal bez odpovědi. Gauss jen občas odkazoval na záznam ve svém matematickém deníku ze 17. června 1798 (latinská kryptická věta: Calculus probabilitatis contra La Place defensus (počet pravděpodobnosti bráněný Laplaceovi) a nic jiného). Laplace věc posoudil tak, že Legendre vydal první publikaci, ale Gauss nepochybně tuto metodu předem znal, sám ji použil a také ji sdělil ostatním astronomům dopisem. Metoda nejmenších čtverců se po zveřejnění rychle stala standardní metodou zpracování astronomických nebo geodetických datových souborů.

Gauss použili metodu intenzivně ve svém průzkumu království Hannoveru od triangulace . Dvoudílná práce byla publikována v letech 1821 a 1823 a v roce 1826 doplněk k Theoria combinationis Observationum erroribus minimis obnoxiae (teorie kombinace pozorování podléhajících nejmenším chybám) , ve kterém Gauss zdůvodnil úspěch metody nejmenších čtverců s uvedením, že byl porovnán s jinými metodami, je výpočet úpravy v širokém ohledu optimální. Matematická formulace tohoto tvrzení je známá jako Gaussova-Markowova věta, pojmenovaná podle Andreje Andrejewitsche Markowa , který tuto část Gaussovy práce, která byla zpočátku opomíjena, znovu objevila a zlidověla ve 20. století (viz také Gauß-Markowova věta # Geschichte ) . Theoria Combinationis také obsahuje metody pro efektivní řešení soustavy lineárních rovnic , jako je například metoda Gauss-Seidel a LR rozkladu , které představují významný pokrok na matematické znalosti času.

Francouzský zeměměřič André-Louis Cholesky vyvinul během první světové války rozklad Cholesky , což ve srovnání s Gaussovou metodou řešení opět představovalo značný nárůst účinnosti. V 60. letech vyvinul Gene Golub myšlenku řešení vyskytujících se systémů lineárních rovnic pomocí dekompozice QR .

Postup

požadavky

Člověk se dívá na závislou proměnnou, která je ovlivněna jednou nebo více proměnnými. Prodloužení pružiny závisí pouze na použité síle, ale ziskovost společnosti závisí na několika faktorech, jako jsou tržby , různé náklady nebo vlastní kapitál . Pro zjednodušení zápisu je reprezentace omezena na jednu proměnnou v následujícím textu . Vztah mezi a proměnnými je určen funkcí modelu , například parabolou nebo exponenciální funkcí${\ displaystyle y}$${\ displaystyle x}$${\ displaystyle x}$${\ displaystyle y}$${\ displaystyle f}$

${\ Displaystyle y (x) = f (x; \ alpha _ {1}, \ dotsc, \ alpha _ {m})}$,

které závisí na a na funkčních parametrech. Tato funkce pochází buď ze znalosti uživatele, nebo z více či méně časově náročného hledání modelu; může být nutné použít různé funkce modelu a porovnat výsledky. Jednoduchým případem založeným na stávajících znalostech je například pružina, protože zde je modelovým požadavkem Hookův zákon a tedy lineární funkce s pružinovou konstantou jako jediným parametrem. V obtížnějších případech, jako je například společnost, však musí výběru typu funkce předcházet složitý proces modelování . ${\ displaystyle x}$${\ displaystyle m}$${\ displaystyle \ alpha _ {j}}$

Aby se získaly informace o parametrech, a tedy o konkrétním typu vztahu, jsou pro příslušné dané hodnoty nezávislých proměnných shromažďovány odpovídající pozorovací hodnoty . Parametry slouží k přizpůsobení zvoleného typu funkce těmto pozorovaným hodnotám . Cílem je nyní zvolit parametry tak, aby funkce modelu co nejlépe aproximovala data. ${\ displaystyle n}$${\ displaystyle x_ {i}}$${\ displaystyle x}$${\ displaystyle y_ {i}}$ ${\ Displaystyle (i = 1, \ dotsc, n)}$${\ displaystyle \ alpha _ {j}}$${\ displaystyle y_ {i}}$${\ displaystyle \ alpha _ {j}}$

Gauss a Legendre měli myšlenku vytvořit distribuční předpoklady o chybách měření těchto pozorovacích hodnot. Měly by být v průměru nulové, měly by mít konstantní rozptyl a měly by být stochasticky nezávislé na jakékoli jiné chybě měření . To znamená, že v chybách měření již nejsou žádné systematické informace, tj. Že kolísají kolem nuly čistě náhodou. Chyby měření by navíc měly být normálně distribuovány , což má na jedné straně pravděpodobnostní výhody a na druhé straně zaručuje, že odlehlé hodnoty jsou tak dobré, jak je nemožné. ${\ displaystyle y}$

Aby bylo možné určit parametry podle těchto předpokladů , je obecně nutné, aby existovalo podstatně více datových bodů než parametrů, takže to musí platit. ${\ displaystyle \ alpha _ {j}}$${\ Displaystyle n> m}$

Minimalizace součtu čtverců chyb

Kritérium pro určení aproximace by mělo být zvoleno tak, aby velké odchylky funkce modelu od dat byly váženy těžší než malé. Pokud není možné řešení bez jakýchkoli odchylek, pak je kompromis s celkově nejmenší odchylkou nejlepším obecně použitelným kritériem.

Za tímto účelem je součet druhých mocnin chyb, kterému se také říká součet čtverců chyb (přesněji: součet druhých mocnin zbytků ), definován jako součet čtvercových rozdílů mezi hodnoty modelové křivky a data . ${\ displaystyle f (x_ {i})}$${\ displaystyle y_ {i}}$

Ve vzorci notace s parametry a výsledky ${\ Displaystyle {\ vec {\ alpha}} = (\ alpha _ {1}, \ alpha _ {2}, \ dots, \ alpha _ {m}) \ in \ mathbb {R} ^ {m}}$${\ Displaystyle {\ vec {f}} = (f (x_ {1}, {\ vec {\ alpha}}), \ tečky, f (x_ {n}, {\ vec {\ alpha}})) \ v \ mathbb {R} ^ {n}}$

${\ Displaystyle \ sum _ {i = 1} ^ {n} (f (x_ {i}, {\ vec {\ alpha}}) - y_ {i}) ^ {2} = \ | {\ vec {f }} - {\ vec {y}} \ | _ {2} ^ {2}.}$

Poté by měly být vybrány ty parametry, pro které je součet čtvercových chyb úprav minimální: ${\ displaystyle \ alpha _ {j}}$

${\ Displaystyle \ min _ {\ vec {\ alpha}} \ | {\ vec {f}} - {\ vec {y}} \ | _ {2} ^ {2}.}$

Jak přesně je tento problém minimalizace vyřešen, závisí na typu funkce modelu.

Pokud je pro externí datovou sadu předpovídán součet čtverců chyb, hovoří se o statistice PRESS ( anglický prediktivní reziduální součet čtverců ).

Funkce lineárního modelu

Funkce lineárního modelu jsou lineární kombinace libovolných, obecně nelineárních základních funkcí. U takovýchto modelových funkcí lze problém minimalizace řešit také analyticky pomocí přístupu extrémních hodnot bez iteračních aproximačních kroků. Nejprve je ukázáno několik jednoduchých speciálních případů a příkladů.

Speciální případ jednoduché lineární nejlépe padnoucí přímky

Odvození a postup

Polynom prvního řádu je jednoduchá modelová funkce se dvěma lineárními parametry

${\ Displaystyle f (x) = \ alpha _ {0} + \ alpha _ {1} x}$

Hledáme koeficienty a nejlépe padnoucí přímku pro dané naměřené hodnoty . Odchylky mezi hledanou přímkou ​​a příslušnými naměřenými hodnotami ${\ displaystyle n}$${\ Displaystyle (x_ {1}, y_ {1}), \ dotsc, (x_ {n}, y_ {n})}$${\ displaystyle \ alpha _ {0}}$${\ displaystyle \ alpha _ {1}}$${\ displaystyle r_ {i}}$

${\ displaystyle {\ begin {matrix} r_ {1} = & \ alpha _ {0} + & \ alpha _ {1} x_ {1} -y_ {1} \\ r_ {2} = & \ alpha _ { 0} + & \ alpha _ {1} x_ {2} -y_ {2} \\\ vdots & \ vdots & \ vdots \\ r_ {n} = & \ alpha _ {0} + & \ alpha _ {1 } x_ {n} -y_ {n} \\\ end {matrix}}}$

se nazývají chyby montáže nebo zbytky . Nyní hledáme koeficienty a s nejmenším součtem druhých mocnin chyb ${\ displaystyle \ alpha _ {0}}$${\ displaystyle \ alpha _ {1}}$

${\ Displaystyle \ min _ {\ alpha _ {0}, \ alpha _ {1}} \ sum _ {i = 1} ^ {n} r_ {i} ^ {2}}$.

Velká výhoda přístupu s tímto čtvercem chyb se projeví, když je tato minimalizace provedena matematicky: součtová funkce je chápána jako funkce dvou proměnných a (příchozí naměřené hodnoty jsou číselné konstanty), pak derivace (přesněji: parciální derivace ) funkce vytvořené podle těchto proměnných (tj. a ) a nakonec z této derivace hledaly nulový bod . Výsledkem je lineární systém rovnic${\ displaystyle \ alpha _ {0}}$${\ displaystyle \ alpha _ {1}}$${\ displaystyle \ alpha _ {0}}$${\ displaystyle \ alpha _ {1}}$

${\ Displaystyle {\ begin {aligned} \ textstyle n \ cdot \ alpha _ {0} + \ left (\ sum \ limits _ {i = 1} ^ {n} x_ {i} \ right) \ alpha _ {1 } & = \ textstyle \ sum \ limits _ {i = 1} ^ {n} y_ {i} \\\ textstyle \ left (\ sum \ limits _ {i = 1} ^ {n} x_ {i} \ right ) \ alpha _ {0} + \ left (\ sum \ limits _ {i = 1} ^ {n} x_ {i} ^ {2} \ right) \ alpha _ {1} & = \ textstyle \ sum \ limits _ {i = 1} ^ {n} x_ {i} y_ {i} \ end {zarovnaný}}}$

s řešením

${\ Displaystyle \ alpha _ {1} = {\ frac {\ sum \ nolimits _ {i = 1} ^ {n} (x_ {i} - {\ overline {x}}) y_ {i}} {\ sum \ nolimits _ {i = 1} ^ {n} (x_ {i} - {\ overline {x}}) ^ {2}}} = {\ frac {\ sum \ nolimits _ {i = 1} ^ {n } (x_ {i} - {\ overline {x}}) (y_ {i} - {\ overline {y}})} {\ sum \ nolimits _ {i = 1} ^ {n} (x_ {i} - {\ overline {x}}) ^ {2}}} = {\ frac {SP_ {xy}} {SQ_ {x}}}}$a ,${\ displaystyle \; \ alpha _ {0} = {\ overline {y}} - \ alpha _ {1} {\ overline {x}}}$

kde představuje je součet součinů odchylek mezi a a představuje na součet kvadratických odchylek o . Je aritmetický průměr z hodnot, podle toho. Řešení pro lze také nalézt v nestředěné formě pomocí výtlakové věty${\ displaystyle SP_ {xy}}$${\ displaystyle x}$${\ displaystyle y}$${\ displaystyle SQ_ {x}}$${\ displaystyle x}$${\ displaystyle \ textstyle {\ overline {x}} = {\ frac {1} {n}} \ sum \ nolimits _ {i = 1} ^ {n} x_ {i}}$${\ displaystyle x}$${\ displaystyle {\ overline {y}}}$${\ displaystyle \ alpha _ {1}}$

${\ Displaystyle \ alpha _ {1} = {\ frac {\ sum _ {i = 1} ^ {n} (x_ {i} y_ {i}) - n {\ overline {x}} {\ overline {y }}} {\ left (\ sum _ {i = 1} ^ {n} x_ {i} ^ {2} \ right) -n {\ overline {x}} ^ {2}}}}$

lze specifikovat. Tyto výsledky lze také odvodit pomocí funkcí skutečné proměnné, tj. Bez parciálních derivací.

Příklad s nejlépe padnoucí přímkou

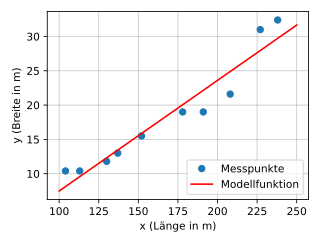
V tomto případě se vypočítá nejlépe padnoucí přímka tvaru, aby se ukázal vztah mezi dvěma vlastnostmi datové sady. Soubor dat se skládá z délky a šířky deseti válečných lodí (viz údaje o válečné lodi ). Měl by být proveden pokus o přiřazení zeměpisné šířky k zeměpisné délce. Data jsou uvedena v prvních třech sloupcích následující tabulky. Ostatní sloupce se týkají průběžných výsledků pro výpočet nejlépe padnoucí přímky. Proměnná by měla označovat délku válečné lodi a její šířku. Hledáme přímku, pro kterou, pokud jsou použity známé hodnoty, jsou funkční hodnoty co nejblíže známým hodnotám . ${\ Displaystyle f (x) = \ alpha _ {0} + \ alpha _ {1} x}$${\ displaystyle x_ {i}}$${\ displaystyle i}$${\ displaystyle y_ {i}}$${\ Displaystyle f (x) = y = \ alpha _ {0} + \ alpha _ {1} x}$${\ displaystyle x_ {i}}$${\ displaystyle f (x_ {i}) = {\ tilde {y}} _ {i}}$${\ displaystyle y_ {i}}$

Válečná loď	Délka (m)	Šířka (m)	${\ displaystyle (x_ {i} - {\ overline {x}})}$	${\ displaystyle (y_ {i} - {\ overline {y}})}$
${\ displaystyle i}$	${\ displaystyle x_ {i}}$	${\ displaystyle y_ {i}}$	${\ displaystyle x_ {i} ^ {*}}$	${\ displaystyle y_ {i} ^ {*}}$	${\ Displaystyle x_ {i} ^ {*} \ cdot y_ {i} ^ {*}}$	${\ displaystyle (x_ {i} ^ {*}) ^ {2}}$	${\ displaystyle f (x_ {i})}$	${\ Displaystyle f (x_ {i}) - y_ {i}}$
1	208	21.6	40.2	3.19	128,24	1616.04	24,88	3,28
2	152	15.5	−15,8	-2,91	45,98	249,64	15,86	0,36
3	113	10.4	−54,8	−8,01	438,95	3003.04	9,57	-0,83
4. místo	227	31.0	59.2	12.59	745,33	3504,64	27,95	−3,05
5	137	13.0	-30,8	−5,41	166,63	948,64	13,44	0,44
6. místo	238	32.4	70.2	13,99	982,10	4928.04	29,72	-2,68
7. místo	178	19.0	10.2	0,59	6.02	104.04	20.05	1,05
8. místo	104	10.4	−63,8	−8,01	511.04	4070,44	8.12	−2,28
9	191	19.0	23.2	0,59	13,69	538,24	22,14	3.14
10	130	11.8	-37,8	-6,61	249,86	1428,84	12.31	0,51
Součet Σ	1678	184,1			3287,72	20391,60

Nejvhodnější linie je určena koeficienty a , které jsou vypočítány pomocí výše uvedeného ${\ displaystyle \ alpha _ {0}}$${\ displaystyle \ alpha _ {1}}$

${\ Displaystyle \ alpha _ {1} = {\ frac {\ sum \ nolimits _ {i = 1} ^ {n} (x_ {i} - {\ overline {x}}) (y_ {i} - {\ overline {y}})} {\ sum \ nolimits _ {i = 1} ^ {n} (x_ {i} - {\ overline {x}}) ^ {2}}} = {\ frac {SP_ {xy }} {SQ_ {x}}}}$

${\ displaystyle \ alpha _ {0} = {\ overline {y}} - \ alpha _ {1} {\ overline {x}}}$

Konstanty a jsou příslušné průměrné hodnoty z - a metriky, takže ${\ displaystyle {\ overline {x}}}$${\ displaystyle {\ overline {y}}}$${\ displaystyle x}$${\ displaystyle y}$

${\ displaystyle {\ overline {x}} = {\ frac {\ sum \ nolimits _ {i = 1} ^ {n} x_ {i}} {n}} = {\ frac {1678} {10}} = 167 {,} 8}$

${\ displaystyle {\ overline {y}} = {\ frac {184.1} {10}} = 18 {,} 41}$

Jako první přechodný krok lze nyní vypočítat odchylku od střední hodnoty pro každou válečnou loď: a - tyto hodnoty se zadávají do čtvrtého a pátého sloupce výše uvedené tabulky. To zjednodušuje vzorec pro${\ displaystyle x_ {i} ^ {*} = (x_ {i} - {\ overline {x}})}$${\ displaystyle \; y_ {i} ^ {*} = (y_ {i} - {\ overline {y}})}$${\ displaystyle \ alpha _ {1}}$

${\ Displaystyle \ alpha _ {1} = {\ frac {\ sum \ nolimits _ {i = 1} ^ {n} x_ {i} ^ {*} \ cdot y_ {i} ^ {*}} {\ sum \ nolimits _ {i = 1} ^ {n} (x_ {i} ^ {*}) ^ {2}}}}$

Jako druhý mezistupeň, produkty a lze vypočítat pro každý válečné. Tyto hodnoty se zadávají v šestém a sedmém sloupci tabulky a nyní je lze snadno sčítat. To lze vypočítat jako ${\ Displaystyle x_ {i} ^ {*} \ cdot y_ {i} ^ {*}}$${\ displaystyle (x_ {i} ^ {*}) ^ {2}}$${\ displaystyle \ alpha _ {1}}$

${\ displaystyle \ alpha _ {1} = {\ frac {3287 {,} 82} {20391 {,} 60}} = 0 {,} 1612}$

Hodnotu lze již interpretovat: Za předpokladu, že data jsou lineárně příbuzná a mohou být popsána naší vypočítanou linií nejlepší shody, se šířka válečné lodi zvětší o přibližně 0,16 metru na každý delší metr. ${\ displaystyle \ alpha _ {1}}$

Zachycení je pak ${\ displaystyle \ alpha _ {0}}$

${\ Displaystyle \ alpha _ {0} = {\ overline {y}} - \ alpha _ {1} {\ overline {x}} = 18 {,} 41-0 {,} 1612 \ cdot 167 {,} 8 = -8 {,} 6451}$

Rovnice nejlépe padnoucí přímky je tedy ${\ displaystyle f (x) = - 8 {,} 6451 + 0 {,} 1612x}$

Pro ilustraci je možné data vykreslit jako bodový graf a vložit nejlépe padnoucí čáru. Graf naznačuje, že mezi délkou a šířkou válečné lodi pro naše ukázková data skutečně existuje lineární vztah. Úprava bodů je celkem dobrá. Na odchylku hodnot předpovězených přímkou od naměřených hodnot lze také pohlížet jako na měřítko . Odpovídající hodnoty se zadávají do osmého a devátého sloupce tabulky. Průměrná odchylka je 2,1 m. Koeficient determinace jako standardizovaný koeficient také udává hodnotu asi 92,2% (100% by odpovídalo střední odchylce 0 m); pro výpočet viz příklad pro koeficient determinace . ${\ Displaystyle f (x_ {i}) - y_ {i}}$${\ displaystyle f (x_ {i})}$${\ displaystyle y_ {i}}$

Negativní zachycení však znamená, že v našem lineárním modelu má válečná loď o délce 0 metrů zápornou šířku - nebo válečné lodě začínají existovat až od určité minimální délky. Ve srovnání s realitou je to samozřejmě špatně, což lze vzít v úvahu při posuzování statistické analýzy. Je pravděpodobné, že model je platný pouze pro oblast, pro kterou jsou naměřené hodnoty skutečně k dispozici (v tomto případě pro délky válečných lodí mezi 100 m a 240 m) a že mimo oblast již není lineární funkce vhodná k reprezentaci data. ${\ displaystyle \ alpha _ {0}}$

Jednoduché polynomové křivky, které nejlépe odpovídají

Nejvhodnější polynomy jsou obecnější než lineární nejlépe padnoucí linie

${\ Displaystyle y (x) \ zhruba \ alpha _ {0} + \ alpha _ {1} x + \ alpha _ {2} x ^ {2} + \ dotsb + \ alpha _ {q} x ^ {q} }$,

což bude nyní ilustrováno na příkladu (takové vyrovnávací polynomické přístupy lze - kromě iteračního řešení - řešit analyticky pomocí přístupu extrémních hodnot).

Výsledky průzkumu Mikrosčítání Federálního statistického úřadu představují průměrné hmotnosti mužů podle věkových skupin (zdroj: Federální statistický úřad, Wiesbaden 2009). Pro analýzu byly věkové skupiny nahrazeny středními třídami. Zkouší se závislost proměnné hmotnosti ( ) na proměnlivém věku ( ). ${\ displaystyle y}$${\ displaystyle x}$

Bodový diagram naznačuje přibližně parabolický vztah mezi a , který lze často dobře aproximovat pomocí polynomu. Stává se polynomickým přístupem k formě ${\ displaystyle x}$${\ displaystyle y}$

${\ Displaystyle y (x) \ cca \ alpha _ {0} + \ alpha _ {1} x + \ alpha _ {2} x ^ {2} + \ alpha _ {3} x ^ {3} + \ alpha _ {4} x ^ {4}}$

zkouší. Řešením je polynom 4. stupně

${\ Displaystyle y (x) \ cca 47 {,} 86 + 2 {,} 2x -0 {,} 04809x ^ {2} +0 {,} 0004935x ^ {3} -0 {,} 000002148x ^ {4} }$.

Měřicí body se odchylují od funkce modelu v průměru ( standardní odchylka ) 0,19 kg. Pokud snížíte stupeň polynomu na 3, získáte řešení

${\ Displaystyle y (x) \ cca 54 {,} 22 + 1 {,} 515x-0 {,} 0226x ^ ​​{2} +0 {,} 0001002x ^ {3}}$

se střední odchylkou 0,22 kg a s polynomickým stupněm 2 roztok

${\ Displaystyle y (x) \ cca 61 {,} 42 + 0 {,} 9397x-0 {,} 008881x ^ {2}}$

s průměrnou odchylkou 0,42 kg. Jak je vidět, pokud jsou vyšší termíny vynechány, změní se koeficienty nižších termínů. Metoda se snaží z každé situace dostat to nejlepší. Odpovídajícím způsobem jsou chybějící vyšší termíny co nejlépe kompenzovány pomocí nižších termínů, dokud není dosaženo matematického optima. Polynom druhého stupně (parabola) velmi dobře popisuje průběh měřicích bodů (viz obrázek).

Zvláštní případ funkce lineárního nastavení s několika proměnnými

Pokud je funkcí modelu vícerozměrný polynom prvního řádu, tj. Pokud má místo jedné proměnné několik nezávislých modelových proměnných , získá se lineární funkce formuláře ${\ displaystyle x}$${\ displaystyle x_ {1}, \ ldots, x_ {N}}$

${\ Displaystyle f (x_ {1}, \ dotsc, x_ {N}; \ alpha _ {0}, \ alpha _ {1}, \ dotsc, \ alpha _ {N}) = \ alpha _ {0} + \ alpha _ {1} x_ {1} + \ dotsb + \ alpha _ {N} x_ {N}}$,

ti na zbytcích

${\ Displaystyle {\ begin {matrix} r_ {1} = & \ alpha _ {0} + \ alpha _ {1} x_ {1,1} + & \ dotsb \; \; + \ alpha _ {j} x_ {j, 1} + & \ dotsb \; \; + \ alpha _ {N} x_ {N, 1} -y_ {1} \\ r_ {2} = α _ {0} + \ alpha _ {1} x_ {1,2} + & \ dotsb \; \; + \ alpha _ {j} x_ {j, 2} + & \ dotsb \; \; + \ alpha _ {N} x_ {N, 2} -y_ {2} \\\ vdots & \ vdots & \ vdots & \ vdots \\ r_ {i} = & \ alpha _ {0} + \ alpha _ {1} x_ {1, i} + & \ dotsb \; \ ; + \ alpha _ {j} x_ {j, i} + & \ dotsb \; \; + \ alpha _ {N} x_ {N, i} -y_ {i} \\\ vdots & \ vdots & \ vdots & \ vdots \\ r_ {n} = α _ {0} + \ alpha _ {1} x_ {1, n} + & \ dotsb \; \; + \ alpha _ {j} x_ {j, n} + & \ dotsb \; \; + \ alpha _ {N} x_ {N, n} -y_ {n} \\\ end {matrix}}}$

vede a o minimalizačním přístupu

${\ Displaystyle \ min _ {\ alpha} \ sum _ {i = 1} ^ {n} r_ {i} ^ {2}}$

lze vyřešit.

Obecný lineární případ

V následujícím textu bude uveden obecný případ všech funkcí lineárního modelu s libovolnou dimenzí. Pro danou funkci měřené hodnoty

${\ displaystyle y (x_ {1}, x_ {2}, \ dots, x_ {N})}$

s nezávislými proměnnými je optimálně přizpůsobená funkce lineárního modelu ${\ displaystyle N}$

${\ Displaystyle f (x_ {1}, x_ {2}, \ dots, x_ {N}; \ alpha _ {1}, \ alpha _ {2}, \ dots, \ alpha _ {m}) = \ sum _ {j = 1} ^ {m} \ alpha _ {j} \ varphi _ {j} (x_ {1}, x_ {2}, \ tečky, x_ {N})}$

chtěl, jehož kvadratická odchylka by měla být minimální. jsou souřadnice funkcí, lineární vstupní parametry, které mají být určeny, a všechny lineárně nezávislé funkce vybrané pro přizpůsobení problému. ${\ displaystyle x_ {i}}$${\ displaystyle \ alpha _ {j}}$${\ displaystyle \ varphi _ {j}}$

V daných měřicích bodech ${\ displaystyle n}$

${\ Displaystyle (x_ {1,1}, x_ {2,1}, \ dots, x_ {N, 1}; y_ {1}), (x_ {1,2}, x_ {2,2}, \ tečky, x_ {N, 2}; y_ {2}), \ tečky, (x_ {1, n}, x_ {2, n}, \ tečky, x_ {N, n}; y_ {n})}$

jeden získá chyby nastavení

${\ Displaystyle {\ begin {matrix} r_ {1} = & \ alpha _ {1} \ varphi _ {1} (x_ {1,1}, \ tečky, x_ {N, 1}) \; \; + α _ {2} \ varphi _ {2} (x_ {1,1}, \ tečky, x_ {N, 1}) + & \ cdots \; \; \; + \ alpha _ {m} \ varphi _ { m} (x_ {1,1}, \ tečky, x_ {N, 1}) - y_ {1} \\ r_ {2} = & \ alpha _ {1} \ varphi _ {1} (x_ {1, 2}, \ tečky, x_ {N, 2}) \; \; + α _ {2} \ varphi _ {2} (x_ {1,2}, \ tečky, x_ {N, 2}) + & \ cdots \; \; \; + \ alpha _ {m} \ varphi _ {m} (x_ {1,2}, \ dots, x_ {N, 2}) - y_ {2} \\\ vdots & \ vdots & \ vdots & \ vdots \\ r_ {i} = & \ alpha _ {1} \ varphi _ {1} (x_ {1, i}, \ dots, x_ {N, i}) \; \; + α _ {2} \ varphi _ {2} (x_ {1, i}, \ tečky, x_ {N, i}) + & \ cdots \; \; \; + \ alpha _ {m} \ varphi _ {m } (x_ {1, i}, \ tečky, x_ {N, i}) - y_ {i} \\\ vdots & \ vdots & \ vdots & \ vdots \\ r_ {n} = & \ alpha _ {1 } \ varphi _ {1} (x_ {1, n}, \ tečky, x_ {N, n}) \; \; + & \ alpha _ {2} \ varphi _ {2} (x_ {1, n} , \ tečky, x_ {N, n}) + & \ cdots \; \; \; + \ alpha _ {m} \ varphi _ {m} (x_ {1, n}, \ dots, x_ {N, n }) - y_ {n} \\\ end {matrix}}}$

nebo v maticovém zápisu

${\ displaystyle r = A \ alpha -y,}$

kde vektor, který shrnuje matici hodnot základních funkcí , vektor parametrů , parametry a vektorová pozorování, kde . ${\ Displaystyle r \ in \ mathbb {R} ^ {n}}$${\ displaystyle r_ {i}}$ ${\ Displaystyle A \ in \ mathbb {R} ^ {n \ times m}}$${\ Displaystyle A_ {ij}: = \ varphi _ {j} (x_ {1, i}, \ tečky, x_ {N, i})}$${\ Displaystyle \ alpha \ in \ mathbb {R} ^ {m}}$${\ displaystyle \ alpha _ {j}}$${\ Displaystyle y \ in \ mathbb {R} ^ {n}}$${\ displaystyle y_ {i}}$${\ Displaystyle n \ geq m}$

Problém minimalizace pomocí euklidovské normy do

${\ Displaystyle \ min _ {\ alpha} \ sum _ {i = 1} ^ {n} r_ {i} ^ {2} = \ min _ {\ alpha} \ | f (\ alpha) -y \ | _ {2} ^ {2} = \ min _ {\ alpha} \ | A \ alpha -y \ | _ {2} ^ {2}}$

může být formulován v pravidelném případě (tj. má úplnou sloupcovou pozici , takže je pravidelný a tedy invertibilní) pomocí vzorce ${\ displaystyle A}$${\ displaystyle A ^ {T} A}$

${\ Displaystyle \ alpha = (A ^ {T} A) ^ {- 1} A ^ {T} y}$

lze vyřešit jasně analyticky, jak bude vysvětleno v další části. V případě singuláru , pokud není v plném pořadí, systém normálních rovnic není jednoznačně řešitelný, tzn. H. parametr nelze identifikovat (viz Gaussova-Markowova věta # Singulární případ, odhadovatelné funkce ). ${\ displaystyle A}$${\ Displaystyle \ alpha}$

Řešení problému minimalizace

Odvození a postup

Problém minimalizace vzniká, jak ukazuje obecný lineární případ, jako

${\ Displaystyle \ min _ {\ alpha} \ | A \ alpha -y \ | _ {2} ^ {2} = \ min _ {\ alpha} (A \ alpha -y) ^ {T} (A \ alpha -y) = \ min _ {\ alpha} (\ alpha ^ {T} A ^ {T} A \ alpha -2y ^ {T} A \ alpha + y ^ {T} y).}$

Tento problém lze vždy vyřešit. Pokud má matice plné hodnocení , je řešení dokonce jedinečné. Chcete -li určit extrémní bod, vynulování parciálních derivací vzhledem k , ${\ displaystyle A}$${\ displaystyle \ alpha _ {j}}$

${\ Displaystyle \ nabla \ | A \ alpha -y \ | _ {2} ^ {2} = 2 (A \ alpha -y) ^ {T} A,}$

lineární systém normálních rovnic (také Gaussovy normální rovnice nebo normální rovnice )

${\ Displaystyle A ^ {T} A \ alpha = A ^ {T} y,}$

který poskytuje řešení problému minimalizace a obecně musí být řešen numericky. Má úplnou hodnost a je , matice je pozitivní definitivní, takže nalezené extrémy jsou opravdu minimum. Tímto způsobem lze řešení problému minimalizace redukovat na řešení soustavy rovnic. V jednoduchém případě nejlépe padnoucí přímky může být její řešení, jak bylo ukázáno, dokonce dáno přímo jako jednoduchý vzorec. ${\ displaystyle A}$${\ Displaystyle n \ geq m}$${\ displaystyle A ^ {T} A}$

Alternativně lze v reprezentaci použít normální rovnice

${\ Displaystyle A ^ {T} A \ alpha -A ^ {T} y = {\ begin {pmatrix} \ left \ langle \ varphi _ {1}, \ varphi _ {1} \ right \ rangle & \ left \ langle \ varphi _ {1}, \ varphi _ {2} \ right \ rangle & \ cdots & \ left \ langle \ varphi _ {1}, \ varphi _ {m} \ right \ rangle \\\ left \ langle \ varphi _ {2}, \ varphi _ {1} \ right \ rangle & \ left \ langle \ varphi _ {2}, \ varphi _ {2} \ right \ rangle & \ cdots & \ left \ langle \ varphi _ { 2}, \ varphi _ {m} \ right \ rangle \\\ vdots & \ vdots & \ ddots & \ vdots \\\ left \ langle \ varphi _ {m}, \ varphi _ {1} \ right \ rangle & \ left \ langle \ varphi _ {m}, \ varphi _ {2} \ right \ rangle & \ cdots & \ left \ langle \ varphi _ {m}, \ varphi _ {m} \ right \ rangle \\\ end {pmatrix}} {\ begin {pmatrix} \ alpha _ {1} \\\ alpha _ {2} \\\ vdots \\\ alpha _ {m} \ end {pmatrix}} - {\ begin {pmatrix} \ vlevo \ langle y, \ varphi _ {1} \ right \ rangle \\\ left \ langle y, \ varphi _ {2} \ right \ rangle \\\ vdots \\\ left \ langle y, \ varphi _ {m } \ right \ rangle \\\ end {pmatrix}} = 0.}$

vypsat, přičemž na standardní skalární symbolizuje produkt a lze také chápat jako integrál překrytí základních funkcí. Základní funkce je třeba číst jako vektory s diskrétními podpůrnými body v místě pozorování . ${\ Displaystyle \ left \ langle \ cdot, \ cdot \ right \ rangle}$${\ displaystyle \ varphi _ {i}}$${\ Displaystyle {\ vec {\ varphi _ {i}}} = (\ varphi _ {i} (x_ {1,1}, \ dots, x_ {N, 1}), \ varphi _ {i} (x_ {1,2}, \ dots, x_ {N, 2}), \ ldots, \ varphi _ {i} (x_ {1, n}, \ dots, x_ {N, n}))}}$${\ displaystyle n}$${\ Displaystyle y = {\ vec {y}} = (y_ {1}, y_ {2}, \ ldots, y_ {n})}$

Kromě toho lze problém minimalizace dobře analyzovat rozkladem singulárních hodnot . To také motivovalo vyjádření pseudo inverze , zobecnění normální inverze matice . To pak poskytuje pohled na nestandardní lineární systémy rovnic, které umožňují ne stochasticky, ale algebraicky motivovaný koncept řešení.

Numerické zpracování roztoku

Existují dva způsoby řešení problému numericky. Na jedné straně normální rovnice

${\ Displaystyle A ^ {T} A \ alpha = A ^ {T} y}$

které jsou jedinečně řešitelné, má -li matice plnou hodnost. Kromě toho má matice součtu produktů tu vlastnost, že je definitivní , takže její vlastní čísla jsou kladná. Spolu se symetrií toho lze použít k vyřešení problému při použití numerických metod: například s Choleskyho dekompozicí nebo metodou CG . Protože jsou obě metody silně ovlivněny stavem matice, někdy to není doporučený přístup: Pokud je podmínka již špatná, pak je kvadratická špatně podmíněná. V důsledku toho lze chyby zaokrouhlení zesílit do takové míry, že způsobí, že výsledek bude nepoužitelný. Metody regularizace však mohou stav zlepšit. ${\ displaystyle A}$ ${\ displaystyle A ^ {T} A}$${\ displaystyle A ^ {T} A}$${\ displaystyle A}$${\ displaystyle A ^ {T} A}$

Jednou z metod je takzvaná hřebenová regrese , která se vrací k Hoerlovi a Kennardovi (1970). Anglické slovo ridge znamená něco jako hřeben, útes, zpět. Místo špatně podmíněné matice je zde použita lépe podmíněná matice . Zde je rozměrný matice identity. Umění spočívá ve vhodném výběru . Příliš malý zvyšuje výdrž jen málo, příliš velký vede ke zkreslené adaptaci. ${\ displaystyle A ^ {T} A}$${\ Displaystyle A ^ {T} A + \ delta I_ {m}}$${\ displaystyle I_ {m}}$${\ displaystyle m}$${\ Displaystyle \ delta}$${\ Displaystyle \ delta}$${\ Displaystyle \ delta}$

Na druhou stranu původní problém minimalizace poskytuje stabilnější alternativu, protože s malou hodnotou minima má podmínku v řádu velikosti podmínky , s velkými hodnotami čtverce podmínku . K výpočtu řešení se používá rozklad QR , který je generován domácími transformacemi nebo Givensovými rotacemi . Základní myšlenkou je, že ortogonální transformace nemění euklidovskou normu vektoru. Tak to je ${\ displaystyle A}$${\ displaystyle A}$

${\ Displaystyle \ | A \ alpha -y \ | _ {2} = \ | Q (A \ alpha -y) \ | _ {2}}$

pro každou ortogonální matici . K vyřešení problému lze vypočítat rozklad QR , přičemž pravá strana je také transformována přímo. To vede k formě ${\ displaystyle Q}$${\ displaystyle A}$

${\ Displaystyle \ | R \ alpha -Q ^ {T} y \ | _ {2}}$

s , kde je pravý horní trojúhelníková matice . Řešení problému je tedy získáno řešením soustavy rovnic ${\ displaystyle R = {\ begin {pmatrix} {\ tilde {R}} \\ 0 \ end {pmatrix}},}$${\ Displaystyle {\ tilde {R}} \ in \ mathbb {R} ^ {m \ times m}}$

${\ Displaystyle {\ tilde {R}} {\ begin {pmatrix} \ alpha _ {1} \\\ vdots \\\ alpha _ {m} \ end {pmatrix}} = {\ begin {pmatrix} (Q ^ {T} y) _ {1} \\\ vdots \\ (Q ^ {T} y) _ {m} \ end {pmatrix}}.}$

Norma minima pak vyplývá ze zbývajících složek transformované pravé strany, protože související rovnice nelze nikdy splnit kvůli nulovým čarám v . ${\ Displaystyle (Qy) _ {m + 1}, \ dots, (Qy) _ {n},}$${\ displaystyle R}$

Ve statistické regresní analýze , vzhledem k několika proměnným, se hovoří o vícenásobné lineární regresi . Nejběžnější přístup, více lineární model k odhadu než obyčejný odhad nejmenších čtverců nebo obyčejný nejmenší čtverec ( anglicky obyčejný nejmenší čtverec , krátce OLS ) známý. Na rozdíl od běžné metody nejmenších čtverců je generalizovaná metoda nejmenších čtverců, používá se krátký VMKQ ( anglicky generalized nejmenších čtverců , krátce GLS ) v generalizovaném lineárním regresním modelu . V tomto modelu se chybové termíny odchylují od distribučního předpokladu, jako je nekorelace a / nebo homoscedasticita . Naproti tomu u vícerozměrné regrese existuje mnoho hodnot pro každé pozorování , takže místo vektoru je přítomna matice (viz obecný lineární model ). Lineární regresní modely byly intenzivně zkoumány ve statistikách z hlediska teorie pravděpodobnosti. Zejména v ekonometrii jsou například analyzovány komplexní rekurzivně definované lineární strukturní rovnice za účelem modelování ekonomických systémů. ${\ displaystyle x_ {1}, \ ldots, x_ {n}}$ ${\ displaystyle i}$ ${\ Displaystyle (i = 1, \ dots, n)}$ ${\ displaystyle r}$${\ displaystyle y}$${\ displaystyle n \ times r}$${\ displaystyle Y}$

Problémy s omezením

Často jsou známy další informace o parametrech, které jsou formulovány sekundárními podmínkami, které jsou pak k dispozici ve formě rovnic nebo nerovnic. Rovnice se objevují například tehdy, když mají být interpolovány určité datové body. Nerovnosti se objevují častěji, obvykle ve formě intervalů pro jednotlivé parametry. V úvodním příkladu byla zmíněna pružinová konstanta, která je vždy větší než nula a vždy ji lze odhadnout směrem nahoru pro konkrétní uvažovaný případ.

V případě rovnice je lze použít pro rozumně položený problém za účelem transformace původního problému minimalizace do jednoho z nižších dimenzí, jehož řešení automaticky splňuje omezení.

Případ nerovnosti je obtížnější. Problém zde vzniká u lineárních nerovností

${\ Displaystyle \ min _ {\ alpha} \ | {\ vec {f}} - {\ vec {y}} \ | _ {2} \;}$s ,${\ Displaystyle \; l \ leq C \ alpha \ leq u}$${\ Displaystyle C \ in \ mathbb {R} ^ {n \ times n},}$

kde nerovnosti jsou míněny komponentově. Tento problém lze vyřešit jednoznačně jako konvexní a kvadratický optimalizační problém a lze k němu přistoupit například pomocí metod pro řešení takových problémů .

Kvadratické nerovnosti vznikají například při použití Tychonowské regularizace k řešení integrálních rovnic . Rozpustnost zde není vždy dána. Numerické řešení může například probíhat speciálními dekompozicemi QR .

Funkce nelineárního modelu

Základní myšlenka a postup

S příchodem výkonných počítačů získává na důležitosti zejména nelineární regrese. Parametry jsou do funkce zahrnuty nelineárním způsobem. Nelineární modelování v zásadě umožňuje přizpůsobit data libovolné tvarové rovnici . Protože tyto rovnice definují křivky , termíny nelineární regrese a „přizpůsobení křivky“ se většinou používají synonymně. ${\ Displaystyle y = f (\ alpha)}$

Některé nelineární problémy lze vhodnou substitucí převést na lineární a poté vyřešit výše uvedeným způsobem. Multiplikativní model formuláře

${\ Displaystyle y = \ alpha _ {0} \ cdot x ^ {\ alpha _ {1}}}$

lze převést na aditivní systém například pomocí logaritmu . Tento přístup se používá mimo jiné v teorii růstu .

Obecně problém tvaru vzniká při nelineárních modelových funkcích

${\ Displaystyle \ min _ {\ alpha} \ | f (\ alpha) -y \ | _ {2},}$

s nelineární funkcí . Dílčí diferenciace pak vede k systému normálních rovnic, které již nelze analyticky řešit. Numerické řešení lze provést iterativně pomocí Gauss-Newtonovy metody . ${\ displaystyle f}$

Současné programy často pracují s jednou variantou, algoritmem Levenberg-Marquardt . Zde je legalizace monotónnost přibližného výsledek zaručen. Pokud je v odhadovaných hodnotách větší odchylka, je metoda navíc tolerantnější než původní metoda. Obě metody souvisejí s Newtonovou metodou a za vhodných podmínek (počáteční bod je dostatečně blízko místnímu optimu) se obvykle sbíhají čtvercově , tj. Počet správných desetinných míst se v každém kroku zdvojnásobí.

Pokud je diferenciace příliš časově náročná kvůli složitosti objektivní funkce, je jako alternativní řešení k dispozici řada dalších metod, které nevyžadují žádné derivace, viz metody lokální nelineární optimalizace .

Příklad z kinetiky enzymů nelineární modelové funkce

Příkladem regresních modelů, které jsou plně nelineární, je kinetika enzymů . Zde se požaduje, aby chyba byla „pouze“ (rychlost reakce) a ne (koncentrace substrátu), a lze ji tedy použít jako proměnnou. Vztah Lineweaver-Burk je algebraicky správná transformace rovnice Michaelis-Menten , ale její aplikace poskytuje správné výsledky pouze v případě, že naměřené hodnoty neobsahují chyby. To vyplývá ze skutečnosti, že realita vzniká pouze s rozšířeným vztahem Michaelis-Menten ${\ displaystyle y}$${\ Displaystyle \ alpha}$${\ Displaystyle \ alpha}$ ${\ Displaystyle v = V _ {\ mathrm {max}} \ cdot [S] / (K_ {m} + [S])}$

${\ Displaystyle \ nu _ {i} = {\ frac {V _ {\ max} \ left [S_ {i} \ right]} {K_ {m} + \ left [S_ {i} \ right]}}} ( 1 + e_ {i}) \ {\ boldsymbol {\ nu}} _ {i}}$

může být popsán s jako parametr chyb. Tuto rovnici již nelze linearizovat, proto zde musí být řešení určeno iterativně. ${\ displaystyle e_ {i}}$

Nesprávné jednání, pokud nejsou splněny požadavky

Metoda nejmenších čtverců umožňuje za určitých podmínek vypočítat nejpravděpodobnější ze všech parametrů modelu. K tomu musí být vybrán správný model, musí být k dispozici dostatečný počet naměřených hodnot a odchylky naměřených hodnot od modelového systému musí tvořit normální rozdělení . V praxi však lze metodu použít i pro různé účely, pokud tyto požadavky nejsou splněny. Je však třeba poznamenat, že metoda nejmenších čtverců může za určitých nepříznivých podmínek poskytnout zcela nežádoucí výsledky. Například by v měřených hodnotách neměly být žádné odlehlé hodnoty, protože ty zkreslují výsledek odhadu . Navíc multikolinearita mezi odhadovanými parametry je nepříznivá, protože způsobuje numerické problémy. Mimochodem, regresoři, kteří jsou daleko od ostatních, mohou mít také velký vliv na výsledky výpočtu úpravy. Mluví se zde o hodnotách s velkým pákovým efektem ( anglicky High Leverage Value ).

Multikolinearita

Fenomén multikolinearity vzniká, když jsou měření dvou daných proměnných a velmi vysoká korelace téměř lineárně závislé. V lineárním případě to znamená, že determinant matice normální rovnice je velmi malý a naopak norma inverzní je velmi velká; stav z je tedy vážně narušena. Normální rovnice se pak numericky obtížně řeší. Hodnoty řešení mohou být neuvěřitelně velké a dokonce i malé změny v pozorováních způsobují velké změny v odhadech. ${\ displaystyle x_ {i}}$${\ displaystyle x_ {j}}$${\ displaystyle A ^ {T} A}$${\ displaystyle A ^ {T} A}$

Utéct

Hodnoty dat, které „nezapadají do řady měření“, jsou definovány jako odlehlé hodnoty . Tyto hodnoty mají velký vliv na výpočet parametrů a zfalšují výsledek. Aby se tomu zabránilo, musí být data zkontrolována na nesprávná pozorování. Zjištěné odlehlé hodnoty lze například vyřadit z řady měření nebo použít alternativní metody výpočtu odolné vůči odlehlým hodnotám, jako je vážená regrese nebo metoda tří skupin.

V prvním případě se po prvním výpočtu odhadovaných hodnot používají statistické testy ke kontrole, zda v jednotlivých naměřených hodnotách existují odlehlé hodnoty. Tyto naměřené hodnoty jsou poté vyřazeny a odhadované hodnoty jsou znovu vypočítány. Tato metoda je vhodná, pokud existuje jen několik odlehlých hodnot.

Při vážené regresi jsou závislé proměnné váženy v závislosti na jejich zbytcích . Odlehlé hodnoty, d. H. Pozorování s velkými zbytky mají nízkou hmotnost, která může být odstupňována v závislosti na velikosti zbytku. V algoritmu podle Mostellera a Tukeyho (1977), který se nazývá „biweighting“, jsou bezproblémové hodnoty váženy 1 a odlehlé hodnoty 0, což znamená, že odlehlá hodnota je potlačena. V případě vážené regrese je obvykle vyžadováno několik iteračních kroků, dokud se sada identifikovaných odlehlých hodnot již nezmění. ${\ displaystyle y}$

Zobecněné modely nejmenších čtverců

Pokud jsou změkčeny silné požadavky v postupu pro chybové členy, získají se takzvané zobecněné přístupy nejmenších čtverců . Důležité speciální případy pak mají svá vlastní jména, například vážené nejmenší čtverce ( anglicky vážené nejmenší čtverce , krátce WLS ), ve kterých se chyby dále pokládají za nekorelované, ale ne více se stejnou odchylkou. To vede k problému formy

${\ Displaystyle \ | D (A \ alpha -y) \ | _ {2},}$

kde D je diagonální matice . Pokud se odchylky velmi liší, odpovídající normální rovnice mají velmi velkou podmínku , a proto by měl být problém vyřešen přímo.

Pokud někdo dále předpokládá, že chyby v naměřených datech by měly být vzaty v úvahu také ve funkci modelu, výsledkem „celkem nejmenších čtverců“ je formulář

${\ Displaystyle \ min _ {E, r} \ | (E, r) \ | _ {F}, (A + E) \ alpha = b + r,}$

kde je chyba v modelu a chyba je v datech.${\ displaystyle E}$${\ displaystyle r}$

Nakonec existuje také možnost nepoužívat jako základ normální distribuci. To odpovídá například minimalizaci nikoli v euklidovské normě, ale v součtové normě . Takové modely jsou předmětem regresní analýzy .

Částečná regrese nejmenších čtverců (PLS)

Částečná regrese nejmenších čtverců (anglicky Partial Least Squares, PLS) nebo „projekce do latentní struktury“ je multivariační metodou a lze ji použít ke zmenšení dimenze, přičemž podobně jako u regrese hlavních komponent je transformace vstupu i proběhnou cílové proměnné.

literatura

• Åke Björck: Numerické metody pro problémy nejmenších čtverců. SIAM, Philadelphia 1996, ISBN 0-89871-360-9 .
• Walter Großmann: Základy výpočtu ekvalizace. 3. ext. Edice. Springer Verlag, Berlin / Heidelberg / New York 1969, ISBN 3-540-04495-7 .
• Richard J. Hanson, Charles L. Lawson: Řešení problémů nejmenších čtverců. SIAM, Philadelphia 1995, ISBN 0-89871-356-0 .
• Frederick Mosteller , John W. Tukey : Analýza dat a regrese - druhý kurz statistiky. Addison-Wesley, Reading MA 1977, ISBN 0-201-04854-X .
• Gerhard Sacrifice: Numerická matematika pro začátečníky. Úvod pro matematiky, inženýry a počítačové vědce. 4. vydání. Vieweg, Braunschweig 2002, ISBN 3-528-37265-6 .
• Peter Schönfeld: Metody ekonometrie. 2 svazky. Vahlen, Berlín / Frankfurt 1969–1971.
• Eberhard Zeidler (ed.): Kapesní kniha matematiky. Odůvodněné v. V Bronsteinu, KA Semendjajew. Teubner, Stuttgart / Leipzig / Wiesbaden 2003, ISBN 3-8171-2005-2 .
• T. Strutz: Přizpůsobení dat a nejistota (Praktický úvod do vážených nejmenších čtverců a dále). 2. vydání. Springer Vieweg, 2016, ISBN 978-3-658-11455-8 .

webové odkazy

Individuální důkazy

1. ↑ Göttingen. In:  Goettingische inzeráty z naučených věcí / Goettingische inzeráty z naučených věcí / Goettingische naučené reklamy , 23. ledna 1802, s. 1 (online na ANNO ).Šablona: ANNO / údržba / plyn
2. ^ Moritz Cantor :  Gauß: Karl Friedrich G. In: Allgemeine Deutsche Biographie (ADB). Svazek 8, Duncker & Humblot, Leipzig 1878, s. 430-445., Zde s. 436.
3. ↑ Paul Karlson: Kouzlo čísel. Ullstein-Verlag, Berlín-západ. Deváté, přepracované a rozšířené vydání, 1967, s. 390 f.
4. ^ A. Abdulle, Gerhard Wanner : 200 let metod nejmenších čtverců . In: Elements of Mathematics , svazek 57, 2002, s. 45-60, doi: 10,1007 / PL00000559 .
5. ↑ Srov. Moritz Cantor :  Gauß: Karl Friedrich G. In: Allgemeine Deutsche Biographie (ADB). Svazek 8, Duncker & Humblot, Leipzig 1878, s. 430-445., S. 436.
6. ^ Adrien-Marie Legendre: Nouvelles méthodes pour la détermination des orbites des comètes. Paris 1805, s. 72–80 (příloha): Sur la Méthode des moindres quarrés.
7. ^ Carl Friedrich Gauß: Theoria Motus Corporum Coelestium in sectionibus conicis solem ambientium . Göttingen 1809; Carl Haase (transl.): Teorie pohybu nebeských těles, která obíhají kolem Slunce v kuželovitých částech. Hannover 1865.
8. ^ Matice a determinanty .
9. ↑ Vytištěno v Gauß, Werke, svazek X / 1, s. 380.
10. ↑ Abdulle, Wanner: Elements of Mathematics . Svazek 57, 2002, s. 51. S faxovou kopií záznamu deníku.
11. ^ Laplace, citováno z Herman Goldstine: Historie numerické analýzy . Springer, 1977, s. 209.
12. ^ Carl Friedrich Gauß: Theoria combinationis Observationum erroribus minimis obnoxiae. 2 díly. Göttingen 1821–1823 (Commentationes Societatis Regiae Scientiarum Gottingensis recentiores, classis mathematicae, svazek 5.); Supplementum Theoria combinationis Observationum erroribus minimis obnoxiae. Göttingen 1826/28 (Commentationes Societatis Regiae Scientiarum Gottingensis recentiores, classis mathematicae, svazek 6.). Anton Börsch Paul Simon (Ed.): Pojednání o metodě nejmenších čtverců Carl Friedrich Gauss. V německém jazyce. Berlín 1887, Textarchiv - internetový archiv .
13. ↑ Pete Stewart: Možná bychom tomu měli říkat „Lagrangeova eliminace“ . Digest Sunday, 21. června 1991, 30. června 1991, svazek 91, číslo 26.
14. ↑ H. Wirths: Relační matematika v regresi a korelaci . In: Stochastik in der Schule , 1991, číslo 1, s. 34–53
15. ^ Hans R. Schwarz, Norbert Köckler: Numerická matematika. 7. revidováno Edice. Teubner, 2009, doi: 10.1007 / 978-3-8348-9282-9 , ISBN 978-3-8348-9282-9 , s. 141, kapitola 3.6 (Gaussova aproximace), věta 3.23.
16. ↑ AE Hoerl a RW Kennard: Ridge regrese: neobjektivní odhad neortogonálních problémů , Techno Metrics 12 (1970), 55-82.
17. ^ Sabine Van Huffel, Joos Vandewalle: Celkový počet nejmenších čtverců Problém: Výpočtové aspekty a analýza. SIAM Publications, Philadelphia PA 1991, ISBN 0-89871-275-0 .
18. ↑ Martin Plesinger: Problém nejmenších čtverců a redukce dat v AX ≈ B. Disertační práce. ( Memento z 24. července 2012 v internetovém archivu ; PDF; 1,6 MB) TU Liberec a ICS Praha, 2008.
19. ↑ Částečná regrese nejmenších čtverců. 3. srpna 2017, přístup 23. srpna 2021 (německy). 
20. ↑ 1,8. Křížový rozklad - dokumentace scikit -learn 0.24.2. Získaný 23. srpna 2021 .