Analytická geometrie

Analytická geometrie (také vektor geometrie ) je větev geometrie jsou algebraické nástroje (především z lineární algebry ) poskytuje pro řešení geometrické chyby. V mnoha případech umožňuje řešit geometrické úlohy čistě aritmeticky bez použití vizualizace jako pomůcky.

Naproti tomu geometrie, která zavádí své věty na axiomatickém základě bez odkazu na číselný systém, se nazývá syntetická geometrie .

Metody analytické geometrie se používají ve všech přírodních vědách , ale především ve fyzice , jako je například popis planetárních drah . Analytická geometrie se původně zabývala pouze otázkami rovinné a prostorové ( euklidovské ) geometrie. V obecném smyslu však analytická geometrie popisuje afinní prostory libovolných rozměrů nad libovolnými tělesy .

Souřadnicový systém

Souřadnicový systém je zásadní pomůckou v analytické geometrii. V praxi se obvykle používá kartézský souřadnicový systém . U některých jednoduchých otázek, jako je stanovení přímkových křižovatek, zkoumání přímek pro rovnoběžnost nebo výpočet parciálních poměrů , by postačoval šikmý souřadný systém . Kartézský souřadný systém je nepostradatelný pro výpočet vzdáleností nebo úhlů .

Vektory

Mnoho výpočtů analytické geometrie je standardizováno a zjednodušeno metodami vektorového výpočtu. Ačkoli byla veškerá analytická geometrie vynalezena bez vektorů a lze ji samozřejmě stále praktikovat bez vektorů a naopak lze vektorový prostor definovat jako abstraktně-algebraický konstrukt bez geometrických odkazů, použití vektorů v kartézských souřadnicových systémech se jeví tak přirozené, že Lineární algebra a analytická geometrie “na vyšší sekundární úrovni a v matematicko-fyzikálně-technickém pregraduálním studiu obecně jako jeden kurz.

Rovnice souřadnic a parametrů

Složitější geometrické struktury, jako jsou přímky , roviny , kružnice , koule, jsou chápány jako množiny bodů a jsou popsány rovnicemi . Mohou to být souřadnicové rovnice nebo parametrické rovnice.

Implicitní souřadnicová rovnice

Výpočetní výraz, který závisí na souřadnicích, je nastaven na 0.${\ displaystyle (x, y, \ dotsc)}$

Příklad (přímka roviny kreslení)

${\ displaystyle 2x-3y + 7 = 0}$

Explicitní rovnice souřadnic

Jedna ze souřadnic je vyjádřena druhou.

Příklad (úroveň v prostoru)

${\ displaystyle z = 2x-5y + 3}$

Výslovné souřadnicové rovnice mají tu nevýhodu, že je často nutné rozlišovat případy; tak to například je

v rovině nelze zobrazit rovnoběžku s -osou ve formě .${\ displaystyle y}$${\ displaystyle y = mx + t}$

Parametrická rovnice

Vektor polohy libovolného bodu ve struktuře je dán vektorovým aritmetickým výrazem, který obsahuje jeden nebo více parametrů.${\ displaystyle {\ vec {x}} = {\ overrightarrow {OX}}}$${\ displaystyle X}$

Příklad (přímo v místnosti): ${\ displaystyle {\ vec {x}} = {\ begin {pmatrix} 2 \\ - 4 \\ - 3 \ end {pmatrix}} + \ lambda {\ begin {pmatrix} -2 \\ 0 \\ 5 \ konec {pmatrix}}}$

Analytická geometrie roviny

Body v rovině

Každý bod roviny je popsán dvěma souřadnicemi , např. B .. Souřadnice se obvykle nazývají (v tomto pořadí) -coordinate (také: úsečka ) a -coordinate (také: ordinate ). Termíny a jsou také používány . ${\ displaystyle P}$${\ displaystyle P (2 \ mid -1 {,} 5)}$${\ displaystyle x}$${\ displaystyle y}$${\ displaystyle x_ {1}}$${\ displaystyle x_ {2}}$

Kombinované souřadnice bodů tvoří uspořádané páry v plochém případě .

Přímky v rovině

Souřadnicová rovnice (implicitní)

${\ displaystyle n_ {x} x + n_ {y} y + n_ {0} = \, \! 0}$

Jeden také mluví o normálním (en) tvaru rovnice přímky, protože vektor je kolmý (normálně) na přímku.${\ displaystyle {\ begin {pmatrix} n_ {x} \\ n_ {y} \ end {pmatrix}}}$

Parametrická rovnice

${\ displaystyle {\ overrightarrow {OX}} = {\ overrightarrow {OA}} + \ lambda {\ vec {u}}}$

Zde je poziční vektor libovolného, ​​ale pevného bodu na přímce (podpůrný bod); je takzvaný směrový vektor, tj. vektor, jehož směr je rovnoběžný s přímkou.${\ displaystyle {\ overrightarrow {OA}} = {\ vec {A}}}$${\ displaystyle {\ vec {u}}}$

Křivky druhého řádu v rovině

Pomocí (implicitní souřadnice) rovnice druhého stupně

${\ displaystyle Ax ^ {2} + Autor: ^ {2} + Cxy + Dx + Ey + F = 0}$

kuželovitý řez je obecně uveden. V závislosti na hodnotách koeficientů to může být elipsa (speciální případ: kruh ), parabola nebo hyperbola .

Analytická geometrie euklidovského prostoru

Body ve vesmíru

Každý bod v prostoru je určen třemi souřadnicemi , např. B .. Každému bodu je přiřazen jeho poziční vektor , který je spojovacím vektorem mezi počátkem souřadnicového systému a daným bodem. Jeho souřadnice odpovídají bodům , ale jsou psány jako vektor sloupce: ${\ displaystyle P}$${\ displaystyle P = P (4 \ mid -0 {,} 5 \ mid -3)}$${\ displaystyle P}$ ${\ displaystyle {\ overrightarrow {OP}}}$${\ displaystyle P}$

${\ displaystyle {\ overrightarrow {OP}} = {\ begin {pmatrix} 4 \\ - 0 {,} 5 \\ - 3 \ end {pmatrix}}}$

Souřadnice se označují jako -, - a -coordinates nebo -, - and -coordinates (v tomto pořadí) . ${\ displaystyle x}$${\ displaystyle y}$${\ displaystyle z}$${\ displaystyle x_ {1}}$${\ displaystyle x_ {2}}$${\ displaystyle x_ {3}}$

Kombinované souřadnice bodů tvoří v prostorovém případě 3 n-tice .

Přímky ve vesmíru

Souřadnicové rovnice

Přímky v prostoru nelze popsat jedinou souřadnicovou rovnicí. Přímku lze vždy chápat jako průsečík (průnik) dvou rovin a pro jasné definování přímky lze použít souřadnicové rovnice těchto dvou rovin (viz níže).

Parametrická rovnice

${\ displaystyle {\ overrightarrow {OX}} = {\ overrightarrow {OA}} + \ lambda {\ vec {u}}}$

Rovnice má tedy stejný tvar jako v dvourozměrném případě.

Úrovně ve vesmíru

Souřadnicová rovnice (implicitní)

${\ displaystyle n_ {x} x + n_ {y} y + n_ {z} z + n_ {0} = \, \! 0}$

Tento typ rovinné roviny se nazývá normální forma , protože vektor je kolmý (normální) k rovině.${\ displaystyle {\ vec {n}} = {\ začátek {pmatrix} n_ {x} \\ n_ {y} \\ n_ {z} \ konec {pmatrix}}}$

Parametrická rovnice

${\ displaystyle {\ overrightarrow {OX}} = {\ overrightarrow {OA}} + \ lambda {\ vec {u}} + \ mu {\ vec {v}}}$

${\ displaystyle {\ overrightarrow {OA}} = {\ vec {A}}}$je poziční vektor libovolného, ​​ale pevného bodu v rovině (podpůrný bod); a jsou lineárně nezávislé směrové vektory (nebo vektory rozpětí ), tj. vektory rovnoběžné s rovinou, které „rozpínají“ rovinu.${\ displaystyle {\ vec {u}}}$${\ displaystyle {\ vec {v}}}$

Plochy druhého řádu v prostoru

Obecná souřadnicová rovnice druhého stupně

${\ displaystyle Ax ^ {2} + Autor: ^ {2} + Cz ^ {2} + Dxy + Exz + Fyz + Gx + Hy + Iz + J = 0}$

popisuje povrch druhého řádu . Nejdůležitější speciální případy jsou:

Elipsoid , eliptický paraboloid , hyperbolický paraboloid , jednoplášťový hyperboloid , dvouplášťový hyperboloid , kužel , eliptický válec , parabolický válec , hyperbolický válec .

Zevšeobecnění: Analytická geometrie jakéhokoli afinního prostoru

Pojmy analytické geometrie lze zobecnit povolením souřadnic z libovolného těla a libovolných dimenzí .

Pokud je vektorový prostor nad tělem a s přidruženou afinního prostoru , pak rozměrný podprostor může být popsána parametrem rovnicí ${\ displaystyle V}$${\ displaystyle K}$${\ displaystyle R}$${\ displaystyle V}$${\ displaystyle k}$${\ displaystyle R}$

${\ displaystyle {\ overrightarrow {OX}} = {\ overrightarrow {OA}} + \ lambda _ {1} {\ vec {v_ {1}}} + \ dotsb + \ lambda _ {k} {\ vec {v_ {k}}}}$.

Zde je poziční vektor libovolného, ​​ale pevného bodu podprostoru (podpůrného bodu); vektory jsou lineárně nezávislé vektory, což je základna v podprostoru z nichž úvaha podprostor patří. ${\ displaystyle {\ overrightarrow {OA}} = {\ vec {A}}}$${\ displaystyle {\ vec {v_ {1}}}, \ dotsc, {\ vec {v_ {k}}}}$${\ displaystyle V}$${\ displaystyle R}$

For je rovnice přímky, pro rovnici roviny. Pokud je 1 menší než rozměr nebo , mluví se o nadrovině . ${\ displaystyle k = 1}$${\ displaystyle k = 2}$${\ displaystyle k}$${\ displaystyle R}$${\ displaystyle V}$

Analogicky k křivkám druhého řádu (kuželovité úseky) rovinné geometrie a povrchům druhého řádu prostorové geometrie se v -dimenzionálním afinním prostoru , tj. Hyperplošinách druhého řádu (s dimenzí ), považují také takzvané kvadriky. , které jsou vytvořeny souřadnicovými rovnicemi druhého stupně, jsou definovány: ${\ displaystyle n}$${\ displaystyle n-1}$

${\ displaystyle \ sum _ {i = 1} ^ {n} \ sum _ {j = 1} ^ {n} A_ {ij} x_ {i} x_ {j} + \ sum _ {i = 1} ^ { n} B_ {i} x_ {i} + C = 0}$

Typické úlohy v analytické geometrii

Kontrola incidentů

Cílem je určit, zda daný bod patří do dané sady bodů (např. Přímka).

Ve dvojrozměrném prostoru

Jako příklad lze uvést přímku s explicitní rovnicí souřadnic

${\ displaystyle y = 2 \ cdot x-3}$

být viděn jako.

Bod leží na této přímce, jak je vidět vložením souřadnic a (ukázka bodu): ${\ displaystyle P (2 | 1)}$${\ displaystyle x = 2}$${\ displaystyle y = 1}$

${\ displaystyle 1 = 2 \ cdot 2-3}$

Bod však není na přímce. Pro a je jmenovitě ${\ displaystyle S (4 | 2)}$${\ displaystyle x = 4}$${\ displaystyle y = 2}$

${\ displaystyle 2 \ neq 2 \ cdot 4-3}$.

V trojrozměrném prostoru

Je třeba zkontrolovat, zda bod leží na přímce pomocí následujícího formuláře parametrů : ${\ displaystyle Q (-1 \ mid 9 \ mid -2)}$

${\ displaystyle {\ vec {x}} = {\ začátek {pmatrix} -7 \\ 7 \\ - 6 \ konec {pmatrix}} + t {\ začátek {pmatrix} 3 \\ 1 \\ 2 \ konec { pmatrix}}}$ .

Pokud je použit poziční vektor , vede to k následujícím 3 rovnicím: ${\ displaystyle {\ vec {x}}}$${\ displaystyle {\ overrightarrow {OQ}}}$${\ displaystyle Q}$

${\ displaystyle {\ begin {matrix} -1 & = & - 7 & + & t \ cdot 3 & \ Rightarrow & t = 2 \\ 9 & = & 7 & + & t \ cdot 1 & \ Rightarrow & t = 2 \\ - 2 & = & - 6 & + & t \ cdot 2 & \ Rightarrow & t = 2 \\\ end {matrix}}}$

Protože má stejnou hodnotu ve všech třech případech (zde ), leží na přímce. ${\ displaystyle t}$${\ displaystyle 2}$${\ displaystyle Q}$

Určení průniku dvou sad bodů

Určení průsečíku dvou sad bodů (např. Průsečík dvou přímek) se rovná řešení soustavy rovnic . V závislosti na formě, ve které jsou popsány dvě sady bodů, se postup trochu liší:

případ 1

Obě sady bodů jsou dány souřadnicovými rovnicemi.

V tomto případě je průsečík popsán souhrnem souřadnicových rovnic.

Případ 2

Obě sady bodů jsou dány parametrickými rovnicemi.

Průsečík se získá rovnicí pravé strany těchto rovnic.

Případ 3

Jedna z množin bodů je dána souřadnicovou rovnicí, druhá parametrickou rovnicí.

V tomto případě jsou jednotlivé souřadnice rovnice vektorového parametru vloženy do rovnice vektoru.

Ve dvojrozměrném prostoru

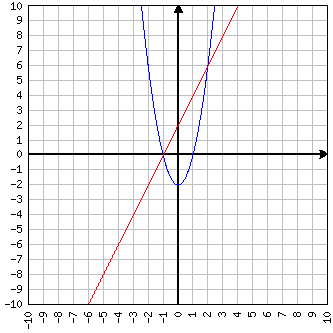
Je třeba zkontrolovat, zda a kde grafy funkcí a protínají. A odpovídá : ${\ displaystyle g (x)}$${\ displaystyle f (x)}$${\ displaystyle g (x) = 2x ^ {2} -2}$${\ displaystyle f (x) = 2x + 2}$

Za účelem výpočtu průsečíků jsou nyní funkční termíny rovnic obou funkcí stejné. Tímto způsobem jeden najde souřadnici (souřadnice), pro které mají obě funkce stejnou souřadnici: ${\ displaystyle x}$${\ displaystyle y}$

${\ displaystyle {\ begin {matrix} 2x ^ {2} & - & 2 & = & 2 \ cdot x & + & 2 \\ 2x ^ {2} & - & 2 \ cdot x & - & 4 & = & 0 \\ x ^ {2} & - & x & - & 2 & = & 0 \\\ end {matrix}}}$

Řešení této kvadratické funkce vede k řešení: a . ${\ displaystyle x_ {1} = - 1}$${\ displaystyle x_ {2} = 2}$

Jeho dosazením do jedné ze dvou počátečních rovnic vzniknou průsečíky v: a . ${\ displaystyle S_ {1} (- 1 | 0)}$${\ displaystyle S_ {2} (2 | 6)}$

V trojrozměrném prostoru

Je třeba přezkoumat, zda a v jakém okamžiku dvě přímky a protínají. Dvě přímky jsou definovány takto: ${\ displaystyle g_ {1}}$${\ displaystyle g_ {2}}$

${\ displaystyle g_ {1}: \; {\ vec {x}} = {\ begin {pmatrix} 20 \\ - 30 \\ 1200 \\\ end {pmatrix}} + s \ cdot {\ begin {pmatrix} -100 \\ 225 \\ - 3 \\\ konec {pmatrix}} \ qquad \ left (s \ in \ mathbb {R} \ right)}$

${\ displaystyle g_ {2}: \; {\ vec {x}} = {\ begin {pmatrix} -2480 \\ 105 \\ 1167 \\\ end {pmatrix}} + t \ cdot {\ begin {pmatrix} 150 \\ 120 \\ 1 \\\ konec {pmatrix}} \ qquad \ left (t \ in \ mathbb {R} \ right)}$

Stejně jako v dvourozměrném prostoru jsou zde rovnice rovnice rovny:

${\ displaystyle {\ begin {pmatrix} 20 \\ - 30 \\ 1200 \\\ end {pmatrix}} + s \ cdot {\ begin {pmatrix} -100 \\ 225 \\ - 3 \\\ konec {pmatrix }} = {\ begin {pmatrix} -2480 \\ 105 \\ 1167 \\\ end {pmatrix}} + t \ cdot {\ begin {pmatrix} 150 \\ 120 \\ 1 \\\ end {pmatrix}} }$

${\ displaystyle s \ cdot {\ začátek {pmatrix} -100 \\ 225 \\ - 3 \\\ konec {pmatrix}} - t \ cdot {\ začátek {pmatrix} -150 \\ - 120 \\ - 1 \ \\ end {pmatrix}} = {\ begin {pmatrix} -2500 \\ 135 \\ - 33 \\\ end {pmatrix}}}$

Vektorovou rovnici lze rozdělit do následujících 3 rovnic:

${\ displaystyle {\ begin {array} {ccccl | l} -100 \ krát s & - & 150 \ krát t & = & - 2500 & \ krát 3/50 \\ 225 \ krát s & - & 120 \ krát t & = & 135 &: 5 \\ -3 \ cdot s & - & 1 \ cdot t & = & - 33 & \ cdot (-2) \\\ end {pole}} \ Leftrightarrow {\ begin {pole} { ccccl} -6 \ cdot s & - & 9 \ cdot t & = & -150 \\ 45 \ cdot s & - & 24 \ cdot t & = & 27 \\ 6 \ cdot s & + & 2 \ cdot t & = & 66 \\\ konec {pole}}}$

Přidáním první a poslední rovnice se získá výtěžek nebo . Z první rovnice takto za následek použitím tak . Toto řešení také splňuje druhou rovnici, protože . ${\ displaystyle -7 \ cdot t = -84}$${\ displaystyle t = 12}$${\ displaystyle -6 \ cdot s = -42}$${\ displaystyle s = 7}$${\ Displaystyle 45 \ krát 7-24 \ krát 12 = 27}$

Vektor polohy průsečíku přímek se získá vložením jednoho ze dvou vypočítaných parametrů ( ) do odpovídající přímky ( ): ${\ displaystyle s}$${\ displaystyle g_ {1}}$

${\ displaystyle {\ begin {pmatrix} 20 \\ - 30 \\ 1200 \\\ konec {pmatrix}} + 7 \ cdot {\ begin {pmatrix} -100 \\ 225 \\ - 3 \\\ konec {pmatrix }} = {\ begin {pmatrix} -680 \\ 1545 \\ 1179 \\\ end {pmatrix}} \ Rightarrow S \ left (-680 | 1545 | 1179 \ right)}$

Dějiny

Analytickou geometrii založil francouzský matematik a filozof René Descartes . Za hlavní vylepšení stojí Leonhard Euler , který se zabýval zejména křivkami a povrchy druhého řádu. Vývoj vektorového výpočtu (mimo jiné Hermannem Graßmannem ) umožnil dnes použít vektorovou notaci.

David Hilbert dokázal, že trojrozměrná analytická geometrie je zcela ekvivalentní (syntetické) euklidovské geometrii ve formě, kterou specifikoval . Z praktického hlediska je to mnohem lepší. V první polovině dvacátého století se proto zastával názor, že geometrie ve způsobu, jakým byla učena, protože Euklid měl pouze historický význam.

Nicolas Bourbaki dokonce šel o krok dále: zcela upustil od geometrických konceptů, jako je bod, přímka atd., A zvážil vše, co bylo třeba říci, s léčbou lineární algebry . Jako vždy u Bourbakiho jsou potřeby aplikované matematiky samozřejmě zcela ignorovány.

Viz také

• Dynamická prostorová geometrie
• Kolekce vzorců analytické geometrie
• Rovnice přímky
• Rovinná rovnice
• Kruhová rovnice
• Subtangens

literatura

• Gerd Fischer : Analytická geometrie: Úvod pro nové studenty . Vieweg, 2001
• Wilhelm Blaschke : Analytická geometrie . Springer, 1953

webové odkazy

• Ina Kersten : Analytická geometrie a lineární algebra . Script, University of Göttingen
• Joachim Gräter: Analytická geometrie . Script, University of Potsdam
• A. Filler: Analytical Geometry na Spektrum.de