Plnění místnosti

Místnosti plnění nebo obklady z trojrozměrném prostoru je náplň z trojrozměrného euklidovském prostoru s trojrozměrných struktur. Dvojrozměrné výplně místností se nazývají parkety .

Výplně místností mohou být kompletní, tj. H. celý objem je vyplněn nebo částečně, což vede k zajímavému problému prostorově nejbližšího balení koulí . V mnoha praktických aplikacích existuje zájem na optimalizaci hustoty náplně místnosti, například v obalovém průmyslu . Matematicky abstrahované výplně místností najdete mimo jiné. s křivkami vyplňujícími prostor , kde se k vyplnění prostoru používají fraktální struktury s fraktální dimenzí menší než rozměr prostoru n a větší než n - 1 .

Prostorové výplně s mnohostěnem

Animace vyplňování prostoru z kongruentní kosočtverečné dodekahedry

Animace vyplňování prostoru z kongruentního zkráceného osmistěnu

Prostorové výplně s kongruentním mnohostěnem

Bezproblémové prostor náplň s mnohostěnů je také nazýván obklady v trojrozměrném prostoru . Existuje přesně pět konvexních mnohostěnů, které jsou omezeny pouze pravidelnými mnohostěnmi, kterými lze prostor zaplnit shodným mnohostěnem jednoho druhu:

krychle
trojúhelníkový pravidelný hranol
šestihranný pravidelný hranol
kroucený dvojitý klín ( Johnsonovo tělo J ₂₆ )
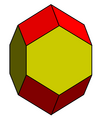
Zkrácený osmistěn

Poslední čtyři mnohostěny obsahují dva typy mnohoúhelníků s různým počtem rohů. Z takzvaných katalánských pevných látek vyplňuje prostor pouze kosočtverec .

krychle
Rovnoběžnostěn
trojúhelníkový pravidelný hranol
šestihranný pravidelný hranol
kroucený dvojitý klín ( Johnsonovo tělo J ₂₆ )
Prodloužený kosočtverečný dvanáctistěn
Kosočtverečný dvanáctistěn
Zkrácený osmistěn

V roce 1885 klasifikoval Evgraf Stepanowitsch Fjodorow parallelohedru vyplňující prostor, tj. Mnohostěn , který lze převést na sebe překladem ( afinní typy konvexního parallelohedry ) a našel pět v trojrozměrném prostoru :

To se stalo důležitým pro jeho klasifikaci krystalografických vesmírných skupin .

Místnost se plní platonickými pevnými látkami

Existují dvě výplně místností, které se skládají výhradně z platonických pevných látek :

8 kostek
8 čtyřstěnů a 6 oktaedrů

Výplně místností s různými mnohostěnmi

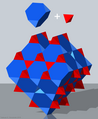
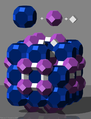
Následující další příklady ukazují, jak lze trojrozměrný prostor zcela vyplnit platonickými tělesy , archimédskými tělesy nebo katalánskými tělesy stejné délky hran. Počet mnohostěnů nutné k vytvoření úplné pevný úhel a je uvedena v každém případě . ${\ displaystyle 4 \ cdot \ pi \ \ mathrm {sr}}$

6 zkrácených čtyřstěnů a 2 čtyřstěnů
4 cuboctahedra a 2 octahedra
4 zkrácené hexahedry a 1 osmistěn
1 zkrácený šestistěn , 1 kosočtverečný kosočtverec , 2 osmiboké hranoly a 1 krychle
3 diamantové cuboctahedry , 1 krychle a 1 čtyřstěn
2 diamantové cuboctahedra , 2 kostky a 1 cuboctahedron
2 zkrácené oktaedry , 2 zkrácené čtyřstěny a 1 cuboctahedron
2 zkrácené cuboctahedra a 2 osmiboké hranoly
2 zkrácený cuboctahedra , 1 zkrácený osmistěn a 1 krychle
2 zkrácený cuboctahedra , 1 zkrácený šestistěn a 1 zkrácený čtyřstěn

Krystalografické omezení

Zajímavý jev se objevuje s periodickým obklady : jejich skupiny symetrie může obsahovat pouze otáčení o 360 °, 180 °, 120 °, 90 ° nebo 60 °, tj prvky na řádů 1, 2, 3, 4 a 6, ale ne rotace o ostatní Úhel , d. H. žádné prvky objednávek 5, 7 nebo vyšších. Tato skutečnost, která mimochodem platí i pro skutečné krystaly , se nazývá krystalografické omezení . Pořadí 5 je však možné u kvazikrystalů, které mají „téměř“ periodické dělení.

Viz také

Individuální důkazy

^ Wolfram MathWorld: Space-Filling Polyhedron
^ Eberhard Scholz, Symmetrie, Gruppe, Dualität, Birkhäuser 1989, s. 117

[1] Wolfram MathWorld: Space-Filling Polyhedron

[2] Eberhard Scholz, Symmetrie, Gruppe, Dualität, Birkhäuser 1989, s. 117

Languages