Desetinný systém

Desetinný systém (od středního latina decimalis , do latiny decem „deset“), také známý jako desítkové systém nebo desítkové systému , je číslo systém , který používá číslo 10 jako báze .

Zpravidla se jím konkrétně rozumí desítkový systém s místním hodnotovým systémem , který byl vyvinut v indických číslicích , předán do evropských zemí prostřednictvím arabské mediace a nyní je celosvětově zaveden jako mezinárodní standard.

Nicméně, desítkové soustavy jsou také číselné systémy založené na 10. Bez systém místo hodnoty, protože jsou založeny na číslicemi mnoha přirozených jazyků a starších číslicemi , někdy ve spojení s quinary , vigesimal nebo jiných číselných soustavách .

Antropologicky je vznik desítkových soustav - a kinetických soustav - spojen s dvakrát 5 prsty člověka . Ty sloužily jako počítací a aritmetické pomůcky ( aritmetika prstů ). Toto vysvětlení je podporováno číslicemi pro 5 („ruka“) a 10 („dvě ruce“) v několika jazycích.

Desetinná soustava hodnot míst

Číslice

V desítkové soustavě se používá deset číslic

0 (nula) , 1 (jedna) , 2 (dvě) , 3 (tři) , 4 (čtyři) , 5 (pět) , 6 (šest) , 7 (sedm) , 8 (osm) , 9 (devět) ,

označované jako desetinné číslice .

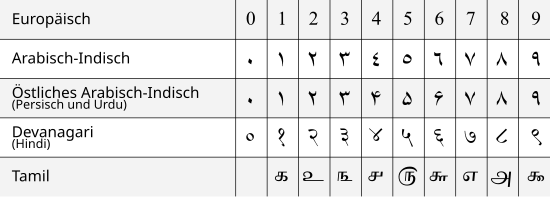
Tyto číslice jsou však v různých částech světa napsány odlišně.

Indické číslice se dodnes používají v různých indických skriptech ( devanagari , bengálské písmo , tamilské písmo atd.). Jsou od sebe velmi odlišní.

definice

V německy mluvícím světě je obvykle ve formě desetinné číslo

${\ Displaystyle z_ {m} \, z_ {m-1} \, \ ldots \, z_ {0} \, \ operatorname {,} \, z _ {- 1} \, z _ {- 2} \, \ ldots \, z _ {- n} \ qquad \ left (m, n \ in \ mathbb {N} \ quad z_ {i} \ in \ {0, \ ldots, 9 \} \ right)}$

zapsáno; Kromě toho existují další hláskování v závislosti na účelu a umístění . Každé je jedním z výše uvedených čísel. Každá číslice má číselnou hodnotu a v závislosti na své poloze hodnotu místa. Číselná hodnota je v běžném pořadí počítání. Index určuje hodnotu, která je mocninou deseti . Číslice jsou psány jeden po druhém bez separátorů, přičemž nejvýznamnější číslici s číslicí na straně zcela vlevo a dolní významné číslice s číslicemi až do napravo od něj v sestupném pořadí. Aby reprezentovaly racionální čísla s neperiodickým vývojem, číslice, které mají následovat po oddělující čárce . V anglicky mluvícím světě se místo čárky používá bod. ${\ displaystyle z_ {i}}$${\ displaystyle i}$${\ displaystyle 10 ^ {i}}$${\ displaystyle z_ {m}}$${\ displaystyle z_ {m-1}}$${\ displaystyle z_ {0}}$${\ displaystyle z _ {- 1}}$${\ displaystyle z _ {- n}}$

Hodnota desítkového čísla se tedy získá sečtením těchto číslic, které se předem vynásobí jejich hodnotou místa; kromě toho má být značka umístěna vpředu; chybějící znak znamená plus: ${\ displaystyle Z}$

${\ Displaystyle Z = \ sum _ {i = -n} ^ {m} z_ {i} \ cdot 10 ^ {i} \ geq 0 \; \ qquad Z = -\ sum _ {i = -n} ^ { m} z_ {i} \ cdot 10 ^ {i} \ leq 0}$.

Tato reprezentace se také nazývá vývoj desetinných zlomků .

Příklad:

${\ Displaystyle 7023 {,} 48 = 7 \ times 10 ^ {3} +0 \ times 10 ^ {2} +2 \ times 10 ^ {1} +3 \ times 10 ^ {0} +4 \ times 10 ^ {-1} +8 \ cdot 10 ^ {- 2}}$

S vyřešenými potencemi získáme:

${\ Displaystyle 7023 {,} 48 = 7 \ cdot 1000 + 0 \ cdot 100 + 2 \ cdot 10 + 3 \ cdot 1 + 4 \ cdot 0 {,} 1 + 8 \ cdot 0 {,} 01}$

Vývoj desetinných zlomků (převod periodických desetinných čísel na zlomky)

Pomocí rozšíření desetinných zlomků můžete ke každému skutečnému číslu přiřadit posloupnost číslic. Každá konečná část této posloupnosti definuje desetinný zlomek , což je aproximace skutečného čísla. Skutečné číslo samotné se získá přesunutím z konečných součtů částí do nekonečné řady přes všechny číslice.

Formálně se nazývá hodnota řady . ${\ Displaystyle z = 0, a_ {1} a_ {2} a_ {3} \ ldots}$${\ Displaystyle \ textstyle \ sum _ {i = 1} ^ {\ infty} a_ {i} 10 ^ {- i}}$

Říká se, že vývoj desetinného zlomku se zastaví, když se posloupnost číslic z pozice n skládá pouze z nul, tj. Skutečné číslo je již samotný desetinný zlomek. Zvláště u všech iracionálních čísel se posloupnost číslic nepřerušuje; existuje nekonečné rozšíření desetinných zlomků.

K transformaci periodické expanze desetinných zlomků se používají následující vztahy:

${\ displaystyle 0 {,} {\ overline {1}} = {\ frac {1} {9}}; \ quad 0 {,} {\ overline {01}} = {\ frac {1} {99}} ; \ quad 0 {,} {\ overline {001}} = {\ frac {1} {999}}; \ quad \ ldots}$.

Tyto identity jsou patrné z pravidel výpočtu pro geometrické řady , která pro použitelné. V prvním příkladu si člověk vybere a nezačne součet, dokud první člen v pořadí. ${\ Displaystyle \ textstyle \ sum _ {i = 0} ^ {\ infty} q ^ {i} = {\ frac {1} {1-q}}}$${\ Displaystyle q <1}$${\ displaystyle q = 10 ^ {- 1}}$

Příklady:

${\ displaystyle 0 {,} 55555 \ ldots = 0 {,} {\ overline {5}} = {\ frac {5} {9}}}$

${\ displaystyle 0 {,} 33333 \ ldots = 0 {,} {\ overline {3}} = {\ frac {3} {9}} = {\ frac {1} {3}}}$

${\ displaystyle 0 {,} 424242 \ ldots = 0 {,} {\ overline {42}} = {\ frac {42} {99}} = {\ frac {14} {33}}}$

${\ displaystyle 0 {,} 081081081 \ ldots = 0 {,} {\ overline {081}} = {\ frac {81} {999}} = {\ frac {3} {37}}}$

Doba se v každém případě přenese na počítadlo . Ve jmenovateli je tolik devítek, kolik je číslic v daném období. V případě potřeby by měla být výsledná přestávka zkrácena .

Výpočet je trochu komplikovanější, pokud období bezprostředně neodpovídá desetinné čárce:

Příklady:

${\ displaystyle 0 {,} 83333 \ ldots = 0 {,} 8 {\ overline {3}} = 8 {,} {\ overline {3}}: 10 = \ left (8 + {\ frac {3} { 9}} \ right): 10 = \ left (8 + {\ frac {1} {3}} \ right): 10 = {\ frac {25} {3}}: 10 = {\ frac {25} { 30}} = {\ frac {5} {6}}}$

${\ Displaystyle 0 {,} 492363636 \ ldots = 0 {,} 492 {\ overline {36}} = 492 {,} {\ overline {36}}: 1000 = 492 {\ frac {36} {99}}: 1000 = 492 {\ frac {4} {11}}: 1000 = {\ frac {5416} {11}}: 1000 = {\ frac {5416} {11000}} = {\ frac {677} {1375}} }$

${\ displaystyle 13 {,} 54323232 \ ldots = 13 {,} 54 {\ overline {32}}}$

1. krok: vynásobíte počáteční číslo mocninou deseti tak, aby přesně jedna tečka (v příkladu 32) byla před desetinnou čárkou:

${\ Displaystyle x = 13 {,} 543232 \ ldots | \ cdot 10 {.} 000}$

${\ Displaystyle 10 {.} 000 \ cdot x = 135 {.} 432 {,} 3232 \ ldots}$

2. krok: potom vynásobíte startovní číslo mocninou deseti, aby tečky začínaly přesně za desetinnou čárkou:

${\ Displaystyle x = 13 {,} 543232 \ ldots | \ cdot 100}$

${\ Displaystyle 100 \ cdot x = 1 {.} 354 {,} 323232 \ ldots}$

3. krok: odečtěte od sebe dva řádky vytvořené v krocích 1 a 2: (tečky za desetinnou čárkou jsou vynechány)

${\ Displaystyle 10 {.} 000 \ cdot x = 135 {.} 432 {,} 323232 \ ldots}$ (Řádek 1)

${\ Displaystyle 100 \ cdot x = 1354 {,} 323232 \ ldots}$ (Řádek 2)

${\ Displaystyle 9 {.} 900 \ cdot x = 135 {.} 432-1 {.} 354 = 134 {.} 078 \!}$ (Řádek 1 mínus řádek 2)

4. krok: přepněte

${\ Displaystyle 9 {.} 900 \ cdot x = 134 {.} 078 |: 9 {.} 900}$

Výsledek: ${\ displaystyle x = {\ frac {134 {.} 078} {9 {.} 900}} = 13 {,} 54 {\ overline {32}}}$

Nejednoznačnost zastoupení

Zvláštností rozšíření desítkové zlomky je, že mnoho racionálních čísel má dvě různá rozšíření desetinných zlomků. Jak je popsáno výše, člověk může změnit tvar a učinit prohlášení ${\ displaystyle 0 {,} {\ overline {9}}}$

${\ displaystyle 0 {,} {\ overline {9}} = {\ frac {9} {9}} = 1}$

dosah, viz článek 0.999 ...

Z této identity lze dále odvodit, že mnoho racionálních čísel (konkrétně všechna s rozšířením konečných desetinných zlomků s výjimkou 0) lze znázornit dvěma různými způsoby: buď jako konečný desetinný zlomek s periodou 0, nebo jako nekonečný desetinný zlomek s tečkou 9. Aby byla reprezentace jednoznačná K tomu můžete jednoduše zakázat období 9 (nebo méně často období 0).

vzorec

Následující vzorec lze nastavit pro periodické desetinné zlomky s nulou před desetinnou čárkou:

${\ Displaystyle p = {\ frac {x \ cdot \ left (10 ^ {n} -1 \ right) + y} {10 ^ {m} \ cdot \ left (10 ^ {n} -1 \ right)} }}$

Zde p je číslo, x je číslo před začátkem období (jako celé číslo), m je počet číslic před začátkem období, y je posloupnost číslic období (jako celé číslo) a n je délka období.

Aplikaci tohoto vzorce je třeba předvést pomocí posledního příkladu:

${\ displaystyle p = 0 {,} 492363636 \ ldots = 0 {,} 492 {\ overline {36}}}$

${\ Displaystyle x = 492; \ quad m = 3; \ quad y = 36; \ quad n = 2}$

${\ Displaystyle p = {\ frac {x \ cdot \ left (10 ^ {n} -1 \ right) + y} {10 ^ {m} \ cdot \ left (10 ^ {n} -1 \ right)} } = {\ frac {492 \ cdot \ left (10 ^ {2} -1 \ right) +36} {10 ^ {3} \ cdot \ left (10 ^ {2} -1 \ right)}} = = { \ frac {492 \ cdot 99 + 36} {1000 \ cdot 99}} = {\ frac {48744} {99000}} = {\ frac {677} {1375}}}$

doba

V matematiky je doba na desetinný zlomek je číslice nebo posloupnost číslic, které se znovu a znovu opakoval za desetinnou čárkou. Všechna racionální čísla , a pouze tato, mají periodické rozšiřování desetinných zlomků.

Příklady:

Čistě periodické: (období začíná bezprostředně za desetinnou čárkou)

1/3 = 0 3 3333 ...

1/7 = 0, 142857 142857 ...

1/9 = 0, 1 1111 ...

Smíšená periodická: (za desetinnou čárkou je předchozí období, než období začíná)

2/55 = 0,0 36 363636 ... (předchozí období 0; délka období 2)

1/30 = 0,0 3 333 ... (předchozí období 0, délka období 1)

1/6 = 0,1 6 666 ... (předchozí období 1, délka období 1)

134078/9900 = 13,54 32 32 ... (předchozí období je 54; délka období je 2)

Mezi periodické desetinné zlomky se počítají také konečné desetinné zlomky; po vložení nekonečného počtu nul, například 0,12 = 0,12000 ...

Skutečná období (tj. Žádné konečné desetinné zlomky) se v desítkové soustavě vyskytují přesně tehdy, když jmenovatel podkladového zlomku nelze generovat výhradně primárními faktory 2 a 5. 2 a 5 jsou hlavní faktory čísla 10, základu desítkové soustavy. Pokud je jmenovatelem prvočíslo (kromě 2 a 5), ​​má období nejvýše délku, která je o jednu menší než hodnota jmenovatele (v příkladech je uvedeno tučně). ${\ displaystyle p}$

Přesná délka doby (v případě, že primární ani 2, ani 5) odpovídá nejmenší přirozené číslo , přičemž na primární faktorizace z vyskytují. ${\ Displaystyle 1 / p}$${\ displaystyle n}$${\ displaystyle p}$${\ displaystyle R_ {n} = {10 ^ {n} -1}}$

Příklad pro délku periody 6 : (10 ⁶ - 1) = 999,999:

999999 = 3 x 3 x 3 x 7 · 11 · 13 · 37 1/ 7 = 0 142857 142857 ... a 1/ 13 = 0, 076 923 076 923 ...

1/7 i 1/13 mají délku periody 6, protože 7 a 13 se objevují poprvé při primární faktorizaci 10 ⁶ - 1. 1/37 má však délku období pouze 3, protože již (10 ³ - 1) = 999 = 3 3 3 37.

Není -li jmenovatelem prvočíslo, délka období odpovídá tomu jako číslo, pro které je jmenovatel poprvé dělitelem ; hlavní faktory 2 a 5 jmenovatele nejsou brány v úvahu. ${\ displaystyle n}$${\ displaystyle R_ {n} = {10 ^ {n} -1}}$

Příklady: 1/185 = 1/(5 * 37) má stejnou délku období jako 1/37, konkrétně 3.

1/143 = 1 / (11 13) má délku období 6, protože 999 999 = 3 3 3 7 143 37 (viz výše)

1/260 = 1/(2 · 2 · 5 · 13) má stejnou délku období jako 1/13, tj. 6.

Aby bylo možné efektivně určit délku období , lze se vyhnout určení primární faktorizace rychle rostoucí číselné řady 9, 99, 999, 9999 atd. Použitím ekvivalentního vztahu , tj. Opakovaného násobení (počínaje 1) o 10 modulo daný jmenovatel , dokud se to opět nerovná 1. Například pro : ${\ displaystyle n}$${\ Displaystyle 10 ^ {n} \ equiv 1 {\ pmod {k}}}$${\ displaystyle k}$${\ displaystyle k = 13}$

${\ Displaystyle 10 ^ {1} \ equiv 10 {\ pmod {13}}}$,

${\ Displaystyle 10 ^ {2} \ equiv 10 \ cdot 10 \ equiv 100 \ equiv 9 {\ pmod {13}}}$,

${\ Displaystyle 10 ^ {3} \ equiv 9 \ cdot 10 \ equiv 90 \ equiv 12 {\ pmod {13}}}$,

${\ Displaystyle 10 ^ {4} \ equiv 12 \ cdot 10 \ equiv 120 \ equiv 3 {\ pmod {13}}}$,

${\ Displaystyle 10 ^ {5} \ equiv 3 \ cdot 10 \ equiv 30 \ equiv 4 {\ pmod {13}}}$,

${\ Displaystyle 10 ^ {6} \ equiv 4 \ cdot 10 \ equiv 40 \ equiv 1 {\ pmod {13}}}$,

1/13 má tedy délku období 6.

notace

U periodických desetinných zlomků je běžný zápis, ve kterém je periodicky se opakující část desetinných míst označena přesahem . příklady jsou

• ${\ displaystyle 1/6 = 0 {,} 1 {\ bar {6}}}$,
• ${\ displaystyle 1/7 = 0 {,} {\ overline {142857}}}$.

Kvůli technickým omezením existují i ​​další konvence. Nadřádek lze umístit vpředu, lze vybrat typografický důraz (tučně, kurzívou, podtržením) periodické části nebo jej lze uvést do závorek:

• 1/6 = 0,1 ¯6 = 0,1 6 = 0,1 6 = 0,1 6 = 0,1 (6)
• 1/7 = 0, ¯ 142857 = 0, 142857 = 0, 142857 = 0, 142857 = 0, (142857)

Neperiodická posloupnost číslic za desetinnou čárkou

Jak je vysvětleno v systému hodnot místa místa , iracionální čísla (také) v desítkové soustavě mají za desetinnou čárkou nekonečnou, neperiodickou posloupnost číslic. Iracionální čísla nemohou být reprezentována konečnou nebo periodickou posloupností číslic. Lze přistupovat s konečnými (nebo periodickými) desetinnými zlomky podle potřeby, ale taková konečná reprezentace není nikdy přesná. Je tedy možné pouze pomocí dalších symbolů označovat iracionální čísla pomocí konečných reprezentací.

Příklady takových symbolů jsou radikální symboly , například pro písmena jako π nebo e , stejně jako matematické výrazy, jako jsou nekonečné řady nebo mezní hodnoty . ${\ displaystyle {\ sqrt {2}}}$

Přeměna na jiné systémy hodnot místa

Metody pro převod z a do desítkové soustavy jsou popsány v článcích o jiných systémech místních hodnot a pod změnou číselné základny a místním hodnotovým systémem .

příběh

Jeden z nejstarších dokladů desítkových kultur vorschriftlicher nalezených v pokladu Oberdingu ze starší doby bronzové (kolem 1650 v. Chr.) Se 791 z velké části standardizovanými sponami z mědi ze Salcburku a Slovenska. Většina těchto tyčí byla umístěna ve skupinách po 10 svazcích.

Desetinné číselné soustavy - stále bez systému místních hodnot a bez zobrazení nul - byly mimo jiné základem číselných skriptů Egypťanů , Minojanů , Řeků a Římanů . Jednalo se o aditivní číselné fonty, pomocí kterých bylo možné čísla zapisovat jako paměťovou pomůcku při výpočtu , ale aritmetické operace v zásadě nebylo možné provádět písemně: jednalo se spíše o mentální aritmetiku nebo o jiné pomůcky, jako je výpočet kamenů (řecky psephoi , Latinské kameny , v pozdním středověku také nazývané aritmetické penny nebo francouzské čipy ) na aritmetice na linkách a případně s čísly prstů .

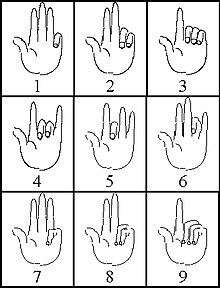
Čísla prstů, která byla v římské a středověké době velmi rozšířená a v arabském světě se také používala v trochu jiné podobě , byla založena na desítkové soustavě pro znázornění čísel 1 až 9999, bez symbolu pro nulu a vlastní polohový systém Pozice prstu na levé ruce s malým, prstenovým a prostředním prstem jednotky 1 až 9 a s ukazováčkem a palcem desítky 10 až 90, zatímco na pravé ruce jsou stovky s palcem a ukazováčkem zrcadlový obraz desítek a tisíců se třemi zbývajícími prsty byl zobrazen jako zrcadlový obraz těch. Říká se, že tato čísla prstů byla použita nejen pro počítání a zapamatování čísel, ale také pro aritmetiku; Současné písemné prameny se však omezují na popis poloh prstů a neposkytují žádné podrobnější informace o matematických operacích, které s nimi lze provádět.

Na druhé straně pro počítadlo řecko-římského starověku a křesťanského středověku byl k dispozici plnohodnotný systém hodnot desetinných míst pro reprezentaci celých čísel, v tom, že pro dané číslo počet jeho jedniček, desítek, stovky atd. byly reprezentovány výpočtem kamenů v odpovídajících svislých desetinných sloupcích. Na starověkém počítadle se to dělo tak, že se do příslušného desetinného sloupce umístil nebo zatlačil odpovídající počet kamenů , přičemž se také procvičovalo svazkování pěti kusů, přičemž pět jednotek bylo vždy reprezentováno jediným kalkulem ve speciální oblasti na boku nebo v horní části desetinného sloupce . Na počitadle kláštera raného středověku, které je dnes většinou spojeno se jménem Gerberts a používalo se od 10. do 12. století, byl počet jednotek v příslušném desetinném sloupci místo toho představován jediným kamenem, který byl kterému předcházelo číslo od 1 do 9, bylo očíslováno, zatímco pozdější středověk a raný novověk se vrátil k používání nečíslovaných aritmetických kamenů a sloupců nebo nyní vodorovně nakreslených čar buď pro desítkovou aritmetiku s celými čísly na základním čísle 10 (s pěti svazky), nebo pro finanční aritmetiku Peněžní základní jednotky zděděné z karolínského ražení mincí (1 libra = 20 solidi = 240 denárů) nedeciálně zarovnané. Na starověkých a středověkých verzích této pomůcky byla hodnota nula zobrazena ponecháním příslušného desetinného sloupce nebo řádku prázdného, ​​a tak také na klášterním počítadle, na kterém byl k dispozici výpočetní kámen s arabskou číslicí (cifra) pro nulu, ale byl použit pro jiné účely v abazistických aritmetických operacích. S pomocí starověkého a středověkého počítadla bylo možné sčítání a odčítání značně zjednodušit, přičemž nebyly příliš vhodné pro rozmnožování a dělení nebo vyžadovaly relativně komplikované operace, které byly popsány zejména pro klášterní počítadlo ve středověkých traktátech a byly proslulé svým obtížnost.

Babyloňané nejprve vyvinuli číselné písmo s plnohodnotným systémem hodnot místa, ve kterém poloha znaku čísla také určuje jeho hodnotu, na základě 60, a pravděpodobně přidal vlastní znak pro nulu již ve 4. století před naším letopočtem . Numerický skript se systémem hodnot místa založený na základně 10, ale stále bez znaku nuly, pravděpodobně vznikl v Číně několik století před přelomem věků (doloženo v detailech od 2. století před naším letopočtem), pravděpodobně s pomoc šachovnice na šachovnici podobné čínské Varianta počítadla, a byla pouze doplněna symbolem pro nulu pod indickým vlivem z 8. století.

V samotné Indii nelze s určitostí určit počátky poziční desítkové soustavy se znaky pro nulu. Starší Brahmiho numerické písmo , které se používalo od 3. do 8. století, používalo desítkovou soustavu s přístupy k pozičnímu psaní, ale stále bez symbolu pro nulu. Nejstarší indická forma dnešních indoarabských číslic se symboly pro 1 až 9 a bodem nebo malým kruhem pro nulu odvozenými ze skriptu Brahmiho čísel je první mimo Indii od 7. století v jihovýchodní Asii v důsledku epigrafických důkazů, že lze bezpečně datovat indický export a lze jej doložit v samotné Indii od 9. století; věří se však, že tento numerický systém se v Indii začal používat již v 5. století. Stejný poziční desítkový systém se znaménky pro nulu byl také základem téměř simultánně naučeného numerického systému indických astronomů, ve kterém popisné výrazy jako „začátek“ (1), „oči“ (2), „tři časové stupně“ (3) u čísel 1 až 9 a „nebe“, „prázdnota“, „bod“ nebo jiná slova pro nulu byly seřazeny podle jejich desetinného místa jako lingvistický popis víceciferných čísel. Lokavibhaga , psaný v Prakrit na 458 , je považován za časný důkaz takové polohové nastavení, v tomto případě do značné míry unmetaphorical jazykových číselné označení , které však má pouze přežily v pozdějším sanskrtského překladu . Soustavu ohraničujících číslic lze plně rozvinout v Bhaskara I (7. století).

Pro psaní čísel Arabové a jimi arabizované národy původně přijaly desítkový aditivní systém abecedních řeckých číslic, zpočátku zprostředkovaný hebrejským a syrským vzorem a přenesený na 28 písmen arabské abecedy. Nejpozději do 8. století se však indické číslice a na nich založené metody výpočtu staly známými nejprve v arabském Orientu a v průběhu 9. století v severní Africe a Al-Andalu . Nejranější zmínku nachází v 7. století syrský biskup Severus Sebokht , který indický systém výslovně chválí. Muhammad ibn Musa al-Chwarizmi , který nejen použil nové číslice ve svých matematických pracích, ale také úvod, pouze v latinském překladu, Kitāb al-Jamʿ wa- hrál důležitou roli v šíření slova v arabštině a západu svět . l-tafrīq bi-ḥisāb al-Hind („O aritmetice s indickými číslicemi“) s popisem numerické soustavy a písemné základní aritmetiky na jejím základě vhodné pro začátečníka .

Ve dnech 10./11. V 19. století se na kalkulačních kamenech klášterního počítadla na latinském západě objevily západní arabské číslice nebo z nich odvozené číslice ( nazývané vrcholy ). Kromě toho však nebyly použity jako číslice ani pro písemnou aritmetiku. Spolu s klášterním počítadlem byli opět zapomenuti. Al-Chwarizmi pomohl indickým číslicím učinit průlom v latinských úpravách a souvisejících pojednáních o lidovém jazyce od 12. století. Jejich počáteční slova Dixit Algorismi zajistila, že „Algorism“, latinský překlad jeho jména, se široce etabloval jako název tohoto nového umění aritmetiky. Zejména v Itálii, kde to Leonardo Fibonacci ve svých Liber Abbaci oznámil ze svých vlastních znalostí získaných v severní Africe, byl indický numerický výpočet schopen téměř úplně vytlačit počítadlo (s výpočetními kameny) ve financích a obchodu od 13. století, a i tak Take names (abbaco) . V jiných zemích se stal předmětem vědecké a obchodní výuky, ale až do raného novověku měl silného konkurenta v aritmetice na linkách. I jako jednoduché číselné písmo pro praktické účely zapisování čísel a číslování , pro které není vyžadován žádný systém hodnot místa, se indoarabské číslice mohly od raného novověku postupně postupně prosazovat proti římským číslicím.

Viz také

• Jména čísel

literatura

• John D. Barrow: Proč je svět matematický / John D. Barrow. Z angličtiny a s doslovem od Herberta Mehrtense . Campus-Verl., Frankfurt / Main 1993, ISBN 3-593-34956-6 . 
• Georges Ifrah: Universal History of Numbers. S kartou a kresbou. autora. Parkland-Verl., Cologne 1998, ISBN 3-88059-956-4 . 
• Karl Menninger: číslo a číslo. Vol. 2. Numerické písmo a aritmetika . Vandenhoeck & Ruprecht, 1958. 
• John M. Pullan: Historie počítadla . Hutchinson, Londýn 1968. 

webové odkazy

• Desetinná soustava / desítky pro školáky vysvětlena na mathematik-wissen.de
• Pochopte systém hodnot desetinných míst a naučte se myslet metakognitivně. Šablony s flexibilními pohovory, to je kritická metoda průzkumu, Piaget

Individuální důkazy

1. ↑ Harald Haarmann: Světová historie čísel . Beck, Mnichov 2008, ISBN 978-3-406-56250-1 , pp. 29 . 
2. ↑ Sledujte A051626 v OEIS
3. ↑ Harald Krause, Sabrina Kutscher a další: Největší evropský barový poklad: měděný poklad starší doby bronzové z Oberdingu. In: Matthias Wemhoff, Michael M. Rind: Moving times: Archaeology in Germany. Berlín, Petersberg 2018, s. 167 a násl.
4. ↑ J. Stolz: První důkaz desítkové soustavy? Poklad barové rané doby bronzové z Oberdingu. In: Restauro. Časopis pro ochranu a restaurování , 8. ročník 2017, s. 14–19.
5. ↑ Menninger: Číselné slovo a číslo (1958), II, s. 3 a dále; Karl-August Wirth, čl. Čísla prstů. In: Otto Schmidt (Ed.): Reallexikon zur deutschen Kunstgeschichte , svazek VIII, Metzler Verlag, Stuttgart 1987, Sp. 1229-1310; Ifrah: Universal History of Numbers (1998), s. 87.
6. ↑ Menninger: číselné slovo a číslo (1958), II, s. 104 a násl .; Ifrah: Universalgeschichte der numbers (1998), s. 136 a další; Pullan, Historie počítadla (1968), s. 16 a násl.
7. ↑ Menninger: číselné slovo a číslo (1958), s. 131ff; Ifrah: Universalgeschichte der numbers (1998), s. 530ff.; Werner Bergmann: Inovace v kvadriviu 10. a 11. století. Studie o zavedení astrolábu a počítadla v latinském středověku , Steiner Verlag, Stuttgart 1985 (= Sudhoffs Archiv, dodatek 26), s. 57 a dále, P. 174 a další.
8. ^ Alfred Nagl: Aritmetické haléře a operační aritmetika. In: Numismatical Journal 19 (1887), s. 309–368; Menninger: číselné slovo a číslo (1958), II, s. 140 a násl .; Pullan: Historie počítadla (1968), passim
9. ^ Francis P. Barnard: Casting Counter a Counting Board. Kapitola v historii numismatiky a rané aritmetiky , Clarendon Press, Oxford 1916; Menninger: číselné slovo a číslo (1958), II, s. 152 a dále, P. 165, s. 178, s. 182f.; Pullan: Historie počítadla (1968), s. 52 a násl .; Ifrah: Univerzální historie čísel (1998), s. 146 a násl.
10. ↑ Ifrah: Universalgeschichte der numbers (1998), s. 411ff., S. 420.
11. ↑ Ifrah: Universalgeschichte der numbers (1998), s. 428ff., P. 511ff.
12. ↑ Ifrah. Univerzální historie čísel (1998), s. 504 a násl.
13. ↑ Ifrah. Univerzální historie čísel (1998), s. 486 a násl.
14. ↑ Ifrah: Universalgeschichte der numbers (1998), s. 498 a další.
15. ↑ Ifrah: Univerzální historie čísel (1998), s. 493 a násl.
16. ↑ Ifrah: Univerzální historie čísel (1998), s. 499f.
17. ↑ Ifrah: Universalgeschichte der numbers (1998), s. 307 a násl.
18. ↑ Ifrah: Universalgeschichte der numbers (1998), s. 533 a další.